题目内容
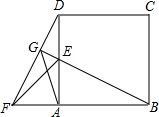 如图,在正方形ABCD的边BA的延长线上作等腰直角△AEF,连接DF,延长BE交DF于G.若FG=6,EG=2,则线段AG的长为
如图,在正方形ABCD的边BA的延长线上作等腰直角△AEF,连接DF,延长BE交DF于G.若FG=6,EG=2,则线段AG的长为考点:全等三角形的判定与性质,等腰直角三角形,正方形的性质
专题:
分析:根据正方形的性质可得AB=AD,等腰直角三角形的性质可得AE=AF,然后利用“边角边”证明△ABE和△ADF全等,根据全等三角形对应边相等可得BE=DF,全等三角形对应角相等可得∠ABE=∠ADG,在BE上截取BH=DG,然后利用“边角边”证明△ABH和△ADG全等,根据全等三角形对应边相等可得AG=AH,全等三角形对应角相等可得∠BAH=∠DAG,求出∠GAH=90°,再判断出△AGH是等腰直角三角形,然后求出FG=EH,再根据等腰直角三角形的性质可得AG=
GH.
| ||
| 2 |
解答:解:在正方形ABCD中,AB=AD,
∵△AEF是等腰直角三角形,
∴AE=AF,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(SAS),
∴BE=DF,∠ABE=∠ADG,
如图,在BE上截取BH=DG,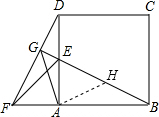
则EH=BE-BH=DF-DG=FG,
在△ABH和△ADG中,
,
∴△ABH≌△ADG(SAS),
∴AG=AH,∠BAH=∠DAG,
∴∠GAH=∠DAG+∠DAH=∠BAH+∠DAH=∠BAD=90°,
∴△AGH是等腰直角三角形,
∵EH=FG=6,EG=2,
∴GH=6+2=8,
∴AG=
GH=
×8=4
.
故答案为:4
.
∵△AEF是等腰直角三角形,
∴AE=AF,
在△ABE和△ADF中,
|
∴△ABE≌△ADF(SAS),
∴BE=DF,∠ABE=∠ADG,
如图,在BE上截取BH=DG,

则EH=BE-BH=DF-DG=FG,
在△ABH和△ADG中,
|
∴△ABH≌△ADG(SAS),
∴AG=AH,∠BAH=∠DAG,
∴∠GAH=∠DAG+∠DAH=∠BAH+∠DAH=∠BAD=90°,
∴△AGH是等腰直角三角形,
∵EH=FG=6,EG=2,
∴GH=6+2=8,
∴AG=
| ||
| 2 |
| ||
| 2 |
| 2 |
故答案为:4
| 2 |
点评:本题考查了全等三角形的判定与性质,正方形的性质,等腰直角三角形的判定与性质,难点在于作辅助线构造出全等三角形和等腰直角三角形.

练习册系列答案
相关题目
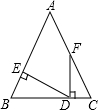 如图,已知△ABC中,∠B=∠C,D为BC上一点,FD⊥BC于D,ED⊥AB于E,∠AFD=150°,∠EDB的度数是( )
如图,已知△ABC中,∠B=∠C,D为BC上一点,FD⊥BC于D,ED⊥AB于E,∠AFD=150°,∠EDB的度数是( )| A、50° | B、40° |
| C、30° | D、60° |
抛物线y=3(x+1)2-2的对称轴是( )
| A、直线x=-2 |
| B、直线x=2 |
| C、直线x=-1 |
| D、直线x=1 |
 如图,已知△ABC中,∠B=90°,角平分线AD、CF相交于E,则∠AEC的度数是
如图,已知△ABC中,∠B=90°,角平分线AD、CF相交于E,则∠AEC的度数是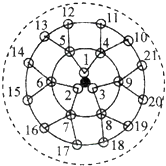 生物课题研究小组对附着在物体表面的三个微生物(课题组成员把他们分别标号为1,2,3)的生长情况进行观察记录,这三个微生物第一天各自一分为二,产生新的微生物(依次被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录),那么标号为1000的微生物会出现在( )
生物课题研究小组对附着在物体表面的三个微生物(课题组成员把他们分别标号为1,2,3)的生长情况进行观察记录,这三个微生物第一天各自一分为二,产生新的微生物(依次被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录),那么标号为1000的微生物会出现在( )