题目内容
在一个不透明的布袋中装有红色、白色玻璃球共60个,除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在25%左右,则口袋中红色球可能有( )
| A、5个 | B、10个 |
| C、15个 | D、45个 |
考点:利用频率估计概率
专题:
分析:由频数=数据总数×频率计算即可.
解答:解:∵摸到红色球的频率稳定在25%左右,
∴口袋中红色球的频率为25%,故红球的个数为60×25%=15(个).
故选:C.
∴口袋中红色球的频率为25%,故红球的个数为60×25%=15(个).
故选:C.
点评:本题考查了利用频率估计概率,难度适中.大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
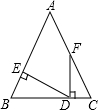 如图,已知△ABC中,∠B=∠C,D为BC上一点,FD⊥BC于D,ED⊥AB于E,∠AFD=150°,∠EDB的度数是( )
如图,已知△ABC中,∠B=∠C,D为BC上一点,FD⊥BC于D,ED⊥AB于E,∠AFD=150°,∠EDB的度数是( )| A、50° | B、40° |
| C、30° | D、60° |
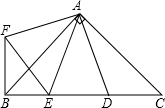 如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①∠EAF=45°;②EF=ED;③BE+DC=DE;④BE2+DC2=DE2.
其中正确的个数有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
若m,n互为相反数,x,y互为倒数,则(m+n)+5xy的值为( )
| A、5 | B、-5 |
| C、0 | D、以上答案都不对 |
下列函数有最大值的是( )
A、y=
| ||
| B、y=-x2 | ||
C、y=-
| ||
| D、y=x2-2 |
 如图,正方形ABCD的面积为4,点F,G分别是AB,DC的中点,将点A折到FG上的点P处,折痕为BE,点E在AD上,则AE长为
如图,正方形ABCD的面积为4,点F,G分别是AB,DC的中点,将点A折到FG上的点P处,折痕为BE,点E在AD上,则AE长为 如图,已知向量
如图,已知向量