题目内容
已知x1、x2是关于x的方程x2-kx+k-1=0的两个实数根,求y=(x1-2x2)(2x1-x2)的最小值.
考点:根与系数的关系,二次函数的最值
专题:
分析:根据根与系数的关系可得出x1+x2、x1x2的值,再化简y=(x1-2x2)(2x1-x2),整体代入,再求最小值.
解答:解:∵x1、x2是关于x的方程x2-kx+k-1=0的两个实数根,
∴x1+x2=k,x1x2=k-1,
∴y=(x1-2x2)(2x1-x2)
=2x12-x1x2-2x1x2+2x22
=2x12-3x1x2+2x22
=2(x12+x22)-3x1x2
=2(x1+x2)2-7x1x2
=2k2-7(k-1)
=2k2-7k+7
=2(k2-
k)+7
=2(k2-
k+
-
)+7
=2(k-
)2+
,
∴y=(x1-2x2)(2x1-x2)的最小值
.
∴x1+x2=k,x1x2=k-1,
∴y=(x1-2x2)(2x1-x2)
=2x12-x1x2-2x1x2+2x22
=2x12-3x1x2+2x22
=2(x12+x22)-3x1x2
=2(x1+x2)2-7x1x2
=2k2-7(k-1)
=2k2-7k+7
=2(k2-
| 7 |
| 2 |
=2(k2-
| 7 |
| 2 |
| 49 |
| 16 |
| 49 |
| 16 |
=2(k-
| 7 |
| 4 |
| 7 |
| 8 |
∴y=(x1-2x2)(2x1-x2)的最小值
| 7 |
| 8 |
点评:本题考查了根与系数的关系以及二次函数的最值,解题的关键是求得两根之和、积,配方法.

练习册系列答案
相关题目
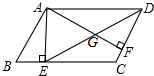 如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥DC于F,∠BAE=30°,BE=2,CF=1.
如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥DC于F,∠BAE=30°,BE=2,CF=1.