题目内容
 如图在梯形ABCD中,两对角线AC、BD互相垂直于O点,且AC=6、BD=8,试求梯形ABCD的中位线MN及高h的长.
如图在梯形ABCD中,两对角线AC、BD互相垂直于O点,且AC=6、BD=8,试求梯形ABCD的中位线MN及高h的长.
分析:过D作DE∥AC,交BC的延长线于E,并延长MN交DE于K,交BD、AC于G、H,那么根据平行四边形的判定可知,四边形ACED是平行四边形,即可得AD=CE,于是梯形的上下底都转化到了△BDE中,即BE=AD+BC,那么MN=
(AD+BC)=
×BE,再根据AC⊥BD,AC∥DE,可证△BDE是直角三角形,利用勾股定理可求BE,从而得出MN,也可以发现,△BDE的面积就等于梯形ABCD的面积,利用三角形的面积公式可求出梯形的高.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:过D作DE∥AC,交BC的延长线于E,并延长MN交DE于K,交BD、AC于G、H,
解:过D作DE∥AC,交BC的延长线于E,并延长MN交DE于K,交BD、AC于G、H,
∵AD∥CE,AC∥DE,
∴四边形ACED是平行四边形,
∴AD=CE,AC=DE,
又∵MN是梯形ABCD的中位线,
∴MN=
(AD+BC),
∴MN=
(CE+BC)=
BE
又∵AC∥DE,AC⊥BD,
∴BD⊥DE,
∴BE=
=
=10,
∴MN=5,
又∵S△BDE=
BD×DE=
BE×h,
∴h=4.8.
 解:过D作DE∥AC,交BC的延长线于E,并延长MN交DE于K,交BD、AC于G、H,
解:过D作DE∥AC,交BC的延长线于E,并延长MN交DE于K,交BD、AC于G、H,∵AD∥CE,AC∥DE,
∴四边形ACED是平行四边形,
∴AD=CE,AC=DE,
又∵MN是梯形ABCD的中位线,
∴MN=
| 1 |
| 2 |
∴MN=
| 1 |
| 2 |
| 1 |
| 2 |
又∵AC∥DE,AC⊥BD,
∴BD⊥DE,
∴BE=
| BD2+DE2 |
| 62+82 |
∴MN=5,
又∵S△BDE=
| 1 |
| 2 |
| 1 |
| 2 |
∴h=4.8.
点评:本题利用了梯形中位线定理、平行四边形的判定和性质、三角形中位线定理、三角形的面积公式等知识.关键是作辅助线,构造平行四边形.

练习册系列答案
相关题目
 如图在梯形ABCD中,AB=DC=10cm,AC与BD相交于G,且∠AGD=60°,设E为CG的中点,F为AB的中点,则EF的长为
如图在梯形ABCD中,AB=DC=10cm,AC与BD相交于G,且∠AGD=60°,设E为CG的中点,F为AB的中点,则EF的长为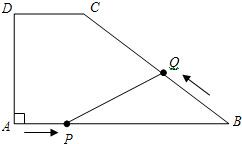 发以3厘米/秒的速度沿B?C?D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为t秒.
发以3厘米/秒的速度沿B?C?D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为t秒. 如图在梯形ABCD中,AD∥BC,E是梯形内一点,ED⊥AD,∠EBC=∠EDC,∠ECB=45°.
如图在梯形ABCD中,AD∥BC,E是梯形内一点,ED⊥AD,∠EBC=∠EDC,∠ECB=45°. (2011•宣城模拟)我们知道连接三角形两边中点的线段叫做三角形的中位线;通过证明可以得到“三角形的中位线平行于三角形的第三边,且等于第三边的一半”类似三角形中位线,我们把连接梯形两腰中点的线段叫做梯形的中位线.如图在梯形ABCD中,AD∥BC,点E,F分别是AB、CD的中点,观察EF的位置,联想三角形中位线的性质,你能发现梯形的中位线有什么性质?证明你的结论.
(2011•宣城模拟)我们知道连接三角形两边中点的线段叫做三角形的中位线;通过证明可以得到“三角形的中位线平行于三角形的第三边,且等于第三边的一半”类似三角形中位线,我们把连接梯形两腰中点的线段叫做梯形的中位线.如图在梯形ABCD中,AD∥BC,点E,F分别是AB、CD的中点,观察EF的位置,联想三角形中位线的性质,你能发现梯形的中位线有什么性质?证明你的结论. 如图在梯形ABCD中,AD∥BC,∠B=∠C,DE交BC于点E,AD=BE.
如图在梯形ABCD中,AD∥BC,∠B=∠C,DE交BC于点E,AD=BE.