题目内容
 如图在梯形ABCD中,AD∥BC,E是梯形内一点,ED⊥AD,∠EBC=∠EDC,∠ECB=45°.
如图在梯形ABCD中,AD∥BC,E是梯形内一点,ED⊥AD,∠EBC=∠EDC,∠ECB=45°.(1)求证:BE=CD;
(2)若梯形ABCD为等腰梯形且DE=3,tan∠DCB=4,试求四边形ABED的周长.
分析:(1)利用作辅助线的方法,证明△BEF和△DCF全等,从而得到BE=CD,
(2)由tan∠DCB=4,根据给出的三角函数的定义,在△DCF中,tan∠DCB=
,过A作AH⊥BC于H,
设EF=CF=x,代入求得x的值,从而求出CD的长,由三角形的全等,CD=BE,证明△AHB≌△DFC,四边形ADFH是矩形,AD=HF,求得答案.
(2)由tan∠DCB=4,根据给出的三角函数的定义,在△DCF中,tan∠DCB=
| DF |
| CF |
设EF=CF=x,代入求得x的值,从而求出CD的长,由三角形的全等,CD=BE,证明△AHB≌△DFC,四边形ADFH是矩形,AD=HF,求得答案.
解答: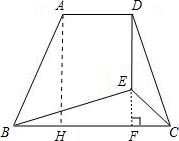 解:(1)延长DE交BC于F,
解:(1)延长DE交BC于F,
∵AD∥BC,
且ED⊥AD,
∴DE⊥BC,
又∵∠ECB=45°,
∴△ECF为等腰直角三角形.
∴EF=CF,((2分)
∴在△BEF和△DCF中
,
∴△BEF≌△DCF,(4分)
∴BE=CD;(5分)
(2)过A作AH⊥BC于H.
设EF=CF=x,
∵Rt△DCF中,
tan∠DCB=
,
∴4=
,
x=1,
∴EF=CF=1,(6分)
∴DF=DE+EF=4,
∴BF=DF=4,
∴在Rt△DFC中,
CD=
=
=
,
∵四边形ABCD为等腰梯形,
∴AB=CD=
,
又∵△BEF≌△DCF,
∴BE=CD=
,(7分)
又∵四边形ABCD为等腰梯形,
∴AB=CD,
又∵AD∥BC且AH⊥BC,DF⊥BC,
∴AH=DF,
∴在Rt△AHB和△DFC中,
,
∴△AHB≌△DFC(HL),(8分)
∴BH=CF=1,
∴HF=BF-BH=4-1=3,(9分)
∴四边形ABED的周长为:AB+BE+DE+AD,
=
+
+3+3,
=6+2
.(10分)
 解:(1)延长DE交BC于F,
解:(1)延长DE交BC于F,∵AD∥BC,
且ED⊥AD,
∴DE⊥BC,
又∵∠ECB=45°,
∴△ECF为等腰直角三角形.
∴EF=CF,((2分)
∴在△BEF和△DCF中
|
∴△BEF≌△DCF,(4分)
∴BE=CD;(5分)
(2)过A作AH⊥BC于H.
设EF=CF=x,
∵Rt△DCF中,
tan∠DCB=
| 3+x |
| x |
∴4=
| 3+x |
| x |
x=1,
∴EF=CF=1,(6分)
∴DF=DE+EF=4,
∴BF=DF=4,
∴在Rt△DFC中,
CD=
| DF2+CF2 |
| 42+12 |
| 17 |
∵四边形ABCD为等腰梯形,
∴AB=CD=
| 17 |
又∵△BEF≌△DCF,
∴BE=CD=
| 17 |
又∵四边形ABCD为等腰梯形,
∴AB=CD,
又∵AD∥BC且AH⊥BC,DF⊥BC,
∴AH=DF,
∴在Rt△AHB和△DFC中,
|
∴△AHB≌△DFC(HL),(8分)
∴BH=CF=1,
∴HF=BF-BH=4-1=3,(9分)
∴四边形ABED的周长为:AB+BE+DE+AD,
=
| 17 |
| 17 |
=6+2
| 17 |
点评:此题是一道梯形和函数综合性的题目,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图在梯形ABCD中,AB=DC=10cm,AC与BD相交于G,且∠AGD=60°,设E为CG的中点,F为AB的中点,则EF的长为
如图在梯形ABCD中,AB=DC=10cm,AC与BD相交于G,且∠AGD=60°,设E为CG的中点,F为AB的中点,则EF的长为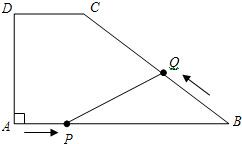 发以3厘米/秒的速度沿B?C?D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为t秒.
发以3厘米/秒的速度沿B?C?D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为t秒. (2011•宣城模拟)我们知道连接三角形两边中点的线段叫做三角形的中位线;通过证明可以得到“三角形的中位线平行于三角形的第三边,且等于第三边的一半”类似三角形中位线,我们把连接梯形两腰中点的线段叫做梯形的中位线.如图在梯形ABCD中,AD∥BC,点E,F分别是AB、CD的中点,观察EF的位置,联想三角形中位线的性质,你能发现梯形的中位线有什么性质?证明你的结论.
(2011•宣城模拟)我们知道连接三角形两边中点的线段叫做三角形的中位线;通过证明可以得到“三角形的中位线平行于三角形的第三边,且等于第三边的一半”类似三角形中位线,我们把连接梯形两腰中点的线段叫做梯形的中位线.如图在梯形ABCD中,AD∥BC,点E,F分别是AB、CD的中点,观察EF的位置,联想三角形中位线的性质,你能发现梯形的中位线有什么性质?证明你的结论. 如图在梯形ABCD中,AD∥BC,∠B=∠C,DE交BC于点E,AD=BE.
如图在梯形ABCD中,AD∥BC,∠B=∠C,DE交BC于点E,AD=BE.