题目内容
20.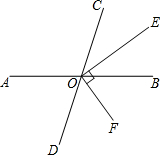 如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,且∠DOF:∠BOE=3:2,求∠AOD的度数.
如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,且∠DOF:∠BOE=3:2,求∠AOD的度数.
分析 根据比例的性质,可用∠BOE表示∠DOF,根据余角的定义,可得关于∠BOE的度数,根据角平分线的定义,可得∠BOC的度数,根据对顶角的性质,可得答案.
解答 解:由∠DOF:∠BOE=3:2,得
∠DOF=$\frac{3∠BOE}{2}$.
由OE平分∠BOC,得∠COE=∠BOE.
由余角的定义,得
∠DOF+∠COE=90°,
即$\frac{3}{2}$∠BOE+∠BOE=90°,
解得∠BOE=36°,
∠BOC=2∠BOE=72°,
由对顶角相等,得
∠AOD=∠BOC=72°.
点评 本题考查了对顶角,利用了比例的性质,利用余角的定义的出关于∠BOE的度数是解题关键,又利用了对顶角的性质.

练习册系列答案
相关题目
 数学课上,小林同学用n个小立方块搭成一个几何体,从三个方向看到的图形如图所示,则n的值是7.
数学课上,小林同学用n个小立方块搭成一个几何体,从三个方向看到的图形如图所示,则n的值是7.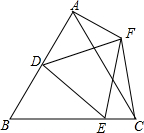 如图,等边△ABC中,D为AB中点,E为BC上一点,以DE为边作等边△DEF,连接CF,AF.
如图,等边△ABC中,D为AB中点,E为BC上一点,以DE为边作等边△DEF,连接CF,AF.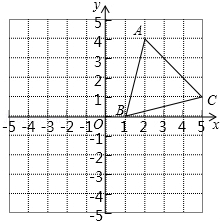 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4)、B(1,0)、C(5,1).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4)、B(1,0)、C(5,1).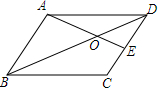 如图,平行四边形ABCD中,E为DC边的中点,AE交BD于O,若BD=6cm,BO=4cm.
如图,平行四边形ABCD中,E为DC边的中点,AE交BD于O,若BD=6cm,BO=4cm.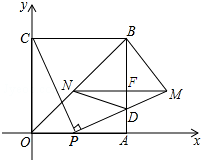 如图,四边形OABC是边长为2的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t.
如图,四边形OABC是边长为2的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t.