题目内容
15.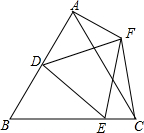 如图,等边△ABC中,D为AB中点,E为BC上一点,以DE为边作等边△DEF,连接CF,AF.
如图,等边△ABC中,D为AB中点,E为BC上一点,以DE为边作等边△DEF,连接CF,AF.(1)求证:FE=FC;
(2)当∠DAF=90°,CE=1时,求等边△ABC的边长.
分析 (1)如图1,连接CD,根据等腰三角形的性质得到CD平分∠ACB,∠DCE=$\frac{1}{2}$∠ACB=30°,作FG⊥DE于G,则FG为DE垂直平分线,于是得到∠DCE=30°=$\frac{1}{2}$∠DFE,证得F为△CDE外接圆圆心,即可得到结论;
(2)如图2,过A、D分别作AI⊥BC,DH⊥BC,借助于平行线分线段成比例定理和全等三角形的判定和性质进行分析求解即可.
解答 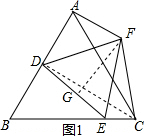 (1)证明:如图1,连接CD,
(1)证明:如图1,连接CD,
∵D为AB中点,
∴CD平分∠ACB,∠DCE=$\frac{1}{2}$∠ACB=30°,
作FG⊥DE于G,则FG为DE垂直平分线,
∴∠DCE=30°=$\frac{1}{2}$∠DFE,
∴F为△CDE外接圆圆心,
∴FE=FC;
(2)解:如图2,过A、D分别作AI⊥BC,DH⊥BC,其垂足分别为I、H,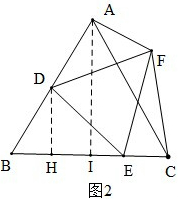
∵△ABC为等边三角形,AI⊥BC,
∴AI垂直平分BC,
∴BI=$\frac{1}{2}$BC,
∵∠ADF+60°+∠BDE=180°,∠BED+60°+∠BDE=180°,
∴∠ADF=∠BED,
在△ADF和△DEB中,$\left\{\begin{array}{l}{∠ADF=∠BED}\\{∠DAD=∠DHE}\\{DF=DE}\end{array}\right.$,
∴△ADF≌△HED(AAS),
∴HE=AD=$\frac{1}{2}$AB=$\frac{1}{2}$BC,
∵DH⊥BC,AI⊥BC,
∴DH∥AI,
∵△ABI中,D为AB中点,DH∥AI,
∴BH=$\frac{1}{2}$BI=$\frac{1}{4}$BC,
BC=CE+HE+BH=1+$\frac{1}{2}$BC+$\frac{1}{4}$BC,
∴BC=4,
即等边△ABC的边长为4.
点评 该题考查了等边三角形的性质和全等三角形的判定和性质,正确的作出辅助线是解答的关键.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案| A. | x=3,y=2 | B. | x=5,y=3 | C. | x=3,y=5 | D. | x=2,y=3 |
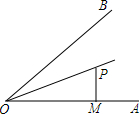 如图,若∠AOB的平分线上一点P到OA的距离PM等于5,N是射线OB上的任一点,则关于PN的长( )
如图,若∠AOB的平分线上一点P到OA的距离PM等于5,N是射线OB上的任一点,则关于PN的长( )| A. | PN>5cm | B. | PN<5cm | C. | PN≥5cm | D. | PN≤5cm |
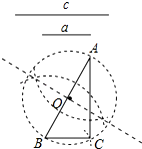 数学课上,老师提出如下问题:已知线段a、c,用尺规作图求作直角三角形ABC,使其斜边AB=c,一条直角边BC=a.小明设计了如下的作图步骤:
数学课上,老师提出如下问题:已知线段a、c,用尺规作图求作直角三角形ABC,使其斜边AB=c,一条直角边BC=a.小明设计了如下的作图步骤:(1)作线段AB=c;
(2)作线段AB的中点O
(3)以O为圆心,OA长为半径作⊙O
(4)以点B为圆心,线段a的长为半径作弧交⊙O于点C
你认为这种作法中判断∠ACB是直角的依据是( )
| A. | 勾股定理 | B. | 直径所对的圆周角是直角 | ||
| C. | 勾股定理的逆定理 | D. | 90°的圆周角所对的弦是直径 |
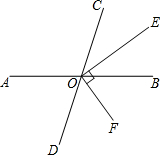 如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,且∠DOF:∠BOE=3:2,求∠AOD的度数.
如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,且∠DOF:∠BOE=3:2,求∠AOD的度数.