题目内容
11.在平面直角坐标系内,A、B、C三点的坐标分别是A(5,0)、B(0,3)、C(10,3),O为坐标原点,点E在线段BC上,若△AEO为等腰三角形,点E的坐标为(2.5,3)或(4,3)或(1,3)或(9,3).分析 先根据等腰三角形的判定画出符合条件的点,根据已知点的坐标和勾股定理求出即可.
解答 解:如图所示: ,
,
符合的有四个点:E1(OE=AE),E2(OE=OA),E3和E4(OA=AE),
∵A(5,0)、B(0,3)、C(10,3),
∴E1(2.5,3),E2(4,3),E3(1,3),E4(9,3),
故答案为:(2.5,3)或(4,3)或(1,3)或(9,3).
点评 本题考查了勾股定理,等腰三角形的判定,点的坐标与图形的应用,能求出符合的所有的情况是解此题的关键,用了分类讨论思想.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
2. 如图,在△ABC中,AB=AC,∠BAC=80°,AD⊥BC于D,则∠B等于( )
如图,在△ABC中,AB=AC,∠BAC=80°,AD⊥BC于D,则∠B等于( )
 如图,在△ABC中,AB=AC,∠BAC=80°,AD⊥BC于D,则∠B等于( )
如图,在△ABC中,AB=AC,∠BAC=80°,AD⊥BC于D,则∠B等于( )| A. | 70° | B. | 50° | C. | 20° | D. | 40° |
19.函数y=x2-6x+13的顶点坐标是( )
| A. | (3,4) | B. | (3,-4) | C. | (-3,-4) | D. | (-3,13) |
1.在平面直角坐标系中,已知点O(0,0)、A(1,$\sqrt{3}$)、B(2,0),点P是线段OB的中点,将△OAB绕点O逆时针旋转30°,记点P的对应点为点Q,则点Q的坐标是( )
| A. | (-$\frac{{\sqrt{3}}}{2}$,-$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,-$\frac{{\sqrt{3}}}{2}$) | C. | ($\frac{{\sqrt{3}}}{2}$,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,$\frac{{\sqrt{3}}}{2}$) |
 如图,已知AB=AC,AB=10cm,CD=3cm,AB的垂直平分线MN交AC于点D,则BD=7cm.
如图,已知AB=AC,AB=10cm,CD=3cm,AB的垂直平分线MN交AC于点D,则BD=7cm.
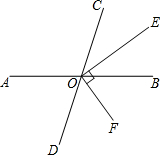 如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,且∠DOF:∠BOE=3:2,求∠AOD的度数.
如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,且∠DOF:∠BOE=3:2,求∠AOD的度数.