题目内容
如图,已知AB为⊙O的直径,CD是弦,且AB CD于点E.连接AC、OC、BC.
CD于点E.连接AC、OC、BC.

(1)求证:∠ACO=∠BCD.
(2)若BE=3,CD=8,求⊙O的直径.
证明:(1)∵AB为⊙O的直径,CD是弦,且AB CD于E,
CD于E,
∴CE=ED, 
∴ BCD=
BCD= BAC.
BAC.
∵OA=OC,
∴ OAC=
OAC= OCA .
OCA .
∴ ACO=
ACO= BCD.
BCD.
(2) ∵CD=8,
∴CE=ED=4,
在Rt BCE中,
BCE中, .
.
∵AB为⊙O的直径,
∴∠ACB=∠BEC=90°.
∵∠B=∠B,
∴△CBE∽△ABC.
∴ .
.
∴
答:⊙O的直径为 .
.
【解析】
试题分析:(1)根据垂径定理得出 ,根据圆周角定理得出∠BCD=∠CAB,根据等腰三角形的性质得出∠CAB=∠ACO,即可得出答案;(2)根据垂径定理求出CE,根据勾股定理求出BC,证出△BCE和△BCA相似,即可得出比例式,代入计算即可求出答案.
,根据圆周角定理得出∠BCD=∠CAB,根据等腰三角形的性质得出∠CAB=∠ACO,即可得出答案;(2)根据垂径定理求出CE,根据勾股定理求出BC,证出△BCE和△BCA相似,即可得出比例式,代入计算即可求出答案.
考点:垂径定理;勾股定理;等腰三角形性质;相似三角形的性质和判定.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(本题满分12分)如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:
朝下数字 | 1 | 2 | 3 | 4 |
出现的次数 | 16 | 20 | 14 | 10 |
(1)计算上述试验中“4朝下”的频率是__________;(3分)
(2)随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于4的概率

 的值.
的值.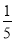 B.
B. C.
C. D.
D.
 知抛物线
知抛物线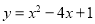 .
.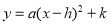 的形式;
的形式;