题目内容
20.(1)先化简,再求值:($\frac{{x}^{2}}{x-3}$+$\frac{9}{3-x}$)÷$\frac{{x}^{2}+6x+9}{x}$,其中x=-1.(2)解不等式组$\left\{\begin{array}{l}{\frac{x+3}{2}>x}\\{x-3(x-1)≤7}\end{array}\right.$,并将其解集表示在数轴上.
分析 (1)根据运算顺序,先算括号里面的,再算除法,分子因式分解,约分即可,再把x=-1代入即可得出答案;
(2)先解两个不等式,再求解集的公共部分,把解集画在数轴上即可.
解答 解:(1)原式=$\frac{{x}^{2}-9}{x-3}$•$\frac{x}{(x+3)^{2}}$
=$\frac{x}{x+3}$,
把x=-1代入原式=$\frac{-1}{-1+3}$=-$\frac{1}{2}$;
(2)$\left\{\begin{array}{l}{\frac{x+3}{2}>x①}\\{x-3(x-1)≤7②}\end{array}\right.$,
解①得x<3,
解②得x≥-2,
把不等式组的解集画在数轴上,
不等式组的解集为-2≤x<3.
点评 本题考查了分式的化简求值以及解一元一次不等式组,分式的通分、因式分解以及不等式组解集的四种情况是解题的关键.

练习册系列答案
相关题目
10.已知二次函数y=$\frac{1}{2}$(x-6)2+3,下列说法:①其图象的开口向下;②其图象的对称轴为直线x=-6;③其图象顶点坐标为(6,3);④当x<6时,y随x的增大而减小.则其中说法正确的是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8. 某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成如表如下:
某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成如表如下:
请根据以上图表提供的信息,解答下列问题:
(1)表中m和n所表示的数分别为:m=90,n=0.3;
(2)请在图中补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段?
(4)若比赛成绩不低于80分可以获奖,则获奖率为多少?
 某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成如表如下:
某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成如表如下:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | m | 0.45 |
| 80≤x<90 | 60 | n |
| 90≤x<100 | 20 | 0.1 |
(1)表中m和n所表示的数分别为:m=90,n=0.3;
(2)请在图中补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段?
(4)若比赛成绩不低于80分可以获奖,则获奖率为多少?
15.对于反比例函数y=$\frac{2}{x}$,下列四个结论正确的是( )
| A. | 图象经过点(2,2) | B. | y随x的增大而减小 | ||
| C. | 图象位于第一、三象限 | D. | 当x<1时,y的值都大于2 |
5.π的相反数是( )
| A. | $\frac{1}{π}$ | B. | -$\frac{1}{π}$ | C. | -π | D. | π |
 如图是一个由若干个棱长为1cm的正方体构成的几何体的三视图,则构成这个几何体的体积是( )cm3.
如图是一个由若干个棱长为1cm的正方体构成的几何体的三视图,则构成这个几何体的体积是( )cm3. 如图,E、F是四边形ABCD的对角线AC上两点,AE=CF,DF∥BE,DF=BE.
如图,E、F是四边形ABCD的对角线AC上两点,AE=CF,DF∥BE,DF=BE.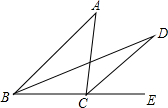 如图,已知△ABC中,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=50°,则∠D=25度.
如图,已知△ABC中,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=50°,则∠D=25度.