题目内容
 如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有( )
如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有( )| A、4条 | B、3条 | C、2条 | D、1条 |
考点:相似三角形的判定
专题:
分析:过点M作直线与另一边相交,使所得的三角形与原三角形有一个公共角,只要再作一个直角就可以.
解答: 解:如图所示,
解:如图所示,
∵△ABC是直角三角形,过M点作直线截△ABC,则截得的三角形与△ABC有一公共角,
∴只要再作一个直角即可使截得的三角形与Rt△ABC相似,过点M可作AB的垂线、AC的垂线、BC的垂线,共3条直线.
故选B.
 解:如图所示,
解:如图所示,∵△ABC是直角三角形,过M点作直线截△ABC,则截得的三角形与△ABC有一公共角,
∴只要再作一个直角即可使截得的三角形与Rt△ABC相似,过点M可作AB的垂线、AC的垂线、BC的垂线,共3条直线.
故选B.
点评:本题考查的是相似三角形的判定,熟知有两组角对应相等的两个三角形相似是解答此题的关键.

练习册系列答案
相关题目
英国曼彻斯热大学的两位科学家因为成功地从石墨中分离出石墨烯,荣获 诺贝尔物理学奖.石墨烯目前是世界上最薄却也是最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.000000000034米,将这个数用科学记数法表示为( )
| A、0.34×10-5 |
| B、3.4×10-4 |
| C、3.4×10-14 |
| D、3.4×10-11 |
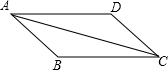 如图,△ABC≌△CDA,下列结论:①AB=CD,BC=DA;②∠BAC=∠DCA,∠ACB=∠CAD;③AB∥CD,BC∥DA,其中正确的个数是( )
如图,△ABC≌△CDA,下列结论:①AB=CD,BC=DA;②∠BAC=∠DCA,∠ACB=∠CAD;③AB∥CD,BC∥DA,其中正确的个数是( )