题目内容
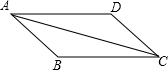如图，△ABC≌△CDA，下列结论：①AB=CD，BC=DA；②∠BAC=∠DCA，∠ACB=∠CAD；③AB∥CD，BC∥DA，其中正确的个数是（ ）| A、0 | B、1 | C、2 | D、3 |
考点：全等三角形的性质
专题：
分析：由三角形全等可得到对应边相等、对应角相等，再结合平行线的判定可判定出三个都正确．
解答：解：∵△ABC≌△CDA，
∴AB=CD，BC=DA；∠BAC=∠DCA，∠ACB=∠CAD；
∴①②正确；
由内错角相等，两直线平行可知AB∥CD，BC∥DA，
∴③正确；
综上可知正确的个数为3，
故选D．
∴AB=CD，BC=DA；∠BAC=∠DCA，∠ACB=∠CAD；
∴①②正确；
由内错角相等，两直线平行可知AB∥CD，BC∥DA，
∴③正确；
综上可知正确的个数为3，
故选D．
点评：本题主要考查全等三角形的性质，掌握全等三角形的对应边、对应角相等是解题的关键．
练习册系列答案
相关题目
计算：（-8）×
×0.125=（ ）
| 3 |
| 5 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
点P关于x轴对称点P1的坐标是（4，-8），则P点关于原点的对称点P2的坐标是（ ）
| A、（-4，-8） |
| B、（4，8） |
| C、（-4，8） |
| D、（4，-8） |
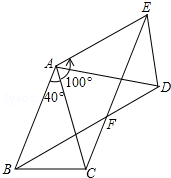如图，△ABC中，AB=AC，∠BAC=40°，将△ABC绕点A按逆时针方向旋转100°．得到△ADE，连接BD，CE交于点F．
在如图所示的平行四边形ABCD中对角线AC．BD交于点O，EF⊥AC，O为垂足，EF分别交AB，CD于点E，F，且BE=OE=
如图，M是Rt△ABC的斜边BC上异于B、C的一定点，过M作直线截△ABC，使截得的三角形与△ABC相似，这样的直线共有（ ）| A、4条 | B、3条 | C、2条 | D、1条 |