题目内容
如图，等腰直角△ABC中，∠ABC=90°，点D在AC上，将△ABD绕顶点B沿顺时针方向旋转90°后得到△CBE.
1.（1）求∠DCE的度数；
2.（2）当AB=4，AD∶DC=1∶3时，求DE的长.
1.解：（1）∵△ABC是等腰直角，∠ABC=90°
∴AB=BC，∠A=∠ACB=45º -----------------------------------1分
∵将△ABD绕顶点B沿顺时针方向旋转90°后得到△CBE
∴△ABD≌△CBE ----------------------------------------2分
∴AD=CE，∠BCE=∠A=45º
∴∠DCE=∠ACB+∠BCE=45º+45º=90º --------------------------3分
2.
(2) ∵BC=AB=4，∠ABC=90°
∴AC=
---------------------------4分
∵AD∶DC=1∶3
∴AD=
,DC=
∴CE=AD= ------------------------------5分
∵∠DCE=90º
∴
∴
-----------------------------------6分
解析:略
练习册系列答案
相关题目
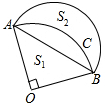如图，等腰直角三角形AOB的面积为S1，以点O为圆心，OA为半径的弧与以AB为直径的半圆围成的图形的面积为S2，则S1与S2的关系是（ ）| A、S1＞S2 | B、S1＜S2 | C、S1=S2 | D、S1≥S2 |
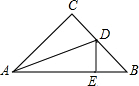如图，等腰直角三角形ABC中，∠C=90°，AD为∠CAB的平分线，DE⊥AB于E，AC=4，则△BDE的周长为（ ）| A、4 | ||
| B、6 | ||
C、4
| ||
D、4
|
（2012•镇江模拟）如图，等腰直角三角形ABC中，AC=BC＞3，点M在AC上，点N在CB的延长线上，MN交AB于点O，且AM=BN=3，则S△AMO与S△BNO的差是（ ）
如图，等腰直角△ABC中，∠ABC=90°，点D在AC上，将△ABD绕顶点B沿顺时针方向旋90°后得到△CBE．
如图，等腰直角三角形△ABC中，∠ACB=90°，点D是BC的中点，CE⊥AD于点F交AB于点E，CH是AB上的高交AD于点G．