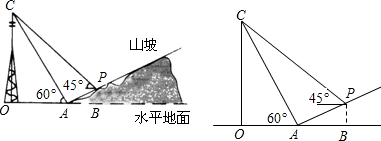
题目内容
 (2012•镇江模拟)如图,等腰直角三角形ABC中,AC=BC>3,点M在AC上,点N在CB的延长线上,MN交AB于点O,且AM=BN=3,则S△AMO与S△BNO的差是( )
(2012•镇江模拟)如图,等腰直角三角形ABC中,AC=BC>3,点M在AC上,点N在CB的延长线上,MN交AB于点O,且AM=BN=3,则S△AMO与S△BNO的差是( )分析:设AC=BC=a,四边形MOBC的面积是x,根据图形得出S△AMO=S△ABC-x,S△BNO=S△NMC-x,求出S△AMO-S△BNO=S△ABC-S△MNC,根据三角形的面积公式代入即可求出答案.
解答:解:∵设AC=BC=a,四边形MOBC的面积是x,
则S△AMO=S△ABC-x,S△BNO=S△NMC-x,
∴S△AMO-S△BNO=(S△ABC-x)-(S△MNC-x)
=S△ABC-S△MNC
=
×a×a-
×(a-3)×(a+3)
=
=4.5,
故选B.
则S△AMO=S△ABC-x,S△BNO=S△NMC-x,
∴S△AMO-S△BNO=(S△ABC-x)-(S△MNC-x)
=S△ABC-S△MNC
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 9 |
| 2 |
故选B.
点评:本题考查了等腰直角三角形性质和三角形的面积的应用,主要考查学生运用性质进行推理和计算的能力.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 (2012•镇江模拟)在8×8的正方形网格中建立如图所示坐标系,已知A(2,4),B(4,2).
(2012•镇江模拟)在8×8的正方形网格中建立如图所示坐标系,已知A(2,4),B(4,2).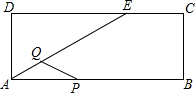 动点Q也从点A出发以每秒1cm的速度向终点E运动.设运动的时间为t秒.解答下列问题:
动点Q也从点A出发以每秒1cm的速度向终点E运动.设运动的时间为t秒.解答下列问题: