题目内容
6.已知f1=$\frac{1}{1-\frac{1}{t}}$,f2=$\frac{1}{1-{f}_{1}}$,f3=$\frac{1}{1-{f}_{2}}$,…,fn+1=$\frac{1}{1-{f}_{n}}$(n为正整数),那么f2016化简后的结果为$\frac{1}{t}$.(结果用t表示)分析 根据f1=$\frac{1}{1-\frac{1}{t}}$,f2=$\frac{1}{1-{f}_{1}}$,f3=$\frac{1}{1-{f}_{2}}$,…,fn+1=$\frac{1}{1-{f}_{n}}$(n为正整数),进行化简可以发现其中的规律,然后根据发现的规律可以得到f2016化简后的结果,从而可以解答本题.
解答 解:∵f1=$\frac{1}{1-\frac{1}{t}}$,f2=$\frac{1}{1-{f}_{1}}$,f3=$\frac{1}{1-{f}_{2}}$,…,fn+1=$\frac{1}{1-{f}_{n}}$(n为正整数),
∴${f}_{1}=\frac{1}{1-\frac{1}{t}}=\frac{t}{t-1}$,${f}_{2}=\frac{1}{1-{f}_{1}}=\frac{1}{1-\frac{t}{t-1}}=1-t$,${f}_{3}=\frac{1}{1-(1-t)}=\frac{1}{t}$,${f}_{4}=\frac{1}{1-\frac{1}{t}}=\frac{t}{t-1}$,…,
∴由上可知,三个一循环,2016÷3=672,
∴f2016=f3=$\frac{1}{t}$.
故答案为:$\frac{1}{t}$.
点评 本题考查分式的混合运算,解题的关键是通过化简前几项发现这组数的规律.

练习册系列答案
相关题目
11.在-1,0,2,$\sqrt{2}$四个数中,最大的数是( )
| A. | -1 | B. | 0 | C. | 2 | D. | $\sqrt{2}$ |
18.已知⊙O是以坐标原点O为圆心,5为半径的圆,点M的坐标为(-3,4),则点M与⊙O的位置关系为( )
| A. | M在⊙O上 | B. | M在⊙O内 | C. | M在⊙O外 | D. | M在⊙O右上方 |
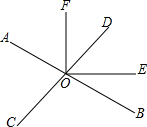 如图,直线AB、CD相交于点O,OE是∠BOD的平分线,如果∠AOC:∠AOD=7:11.
如图,直线AB、CD相交于点O,OE是∠BOD的平分线,如果∠AOC:∠AOD=7:11.