题目内容
14.先化简,再求值:($\frac{a}{a-b}-\frac{{a}^{2}}{{a}^{2}-2ab+{b}^{2}}$)÷($\frac{a}{a+b}-\frac{{a}^{2}}{{a}^{2}-{b}^{2}}$)+1,其中a=2,b=3.分析 先算括号内的减法,再把除法转化为乘法来做,通过分解因式,约分化为最简,最后把数代入计算.
解答 解:原式=$\frac{{a}^{2}-ab-{a}^{2}}{(a-b)^{2}}$÷$\frac{{a}^{2}+ab-{a}^{2}}{(a+b)(a-b)}$+1
=-$\frac{a+b}{a-b}$+1,
当a=2,b=3时,
原式=-$\frac{2+3}{2-3}$+1=5+1=6.
点评 此题考查的是分式的除法和减法的混合运算,有括号的先算括号,还要注意符号的变化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.点P(-5,3)关于y轴的对称点的坐标是( )
| A. | (-5,-3) | B. | (5,-3) | C. | (5,3) | D. | (-5,3) |
19.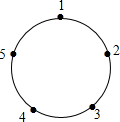 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下列沿顺时针方向跳两个点:若停在偶数点上,则下次沿逆时针方向跳一个点,若青蛙从1这点开始跳,则经过2016次后它停在哪个数对应的点上( )
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下列沿顺时针方向跳两个点:若停在偶数点上,则下次沿逆时针方向跳一个点,若青蛙从1这点开始跳,则经过2016次后它停在哪个数对应的点上( )
 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下列沿顺时针方向跳两个点:若停在偶数点上,则下次沿逆时针方向跳一个点,若青蛙从1这点开始跳,则经过2016次后它停在哪个数对应的点上( )
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下列沿顺时针方向跳两个点:若停在偶数点上,则下次沿逆时针方向跳一个点,若青蛙从1这点开始跳,则经过2016次后它停在哪个数对应的点上( )| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
4.据统计,全球每年约有50万人因患重症登格热需住院治疗,其中很大一部分是儿童患者,数据“50万”用科学记数法表示为( )
| A. | 50×104 | B. | 5×105 | C. | 5×106 | D. | 5×10 |
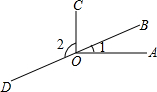 如图,∠1=20°,∠AOC=90°,点B,O,D在同一直线上,则∠2=110°.
如图,∠1=20°,∠AOC=90°,点B,O,D在同一直线上,则∠2=110°.