题目内容
已知∠AOB=60°,点P到射线OA、OB的距离分别为2
和
,垂足分别为M、N,则ON的长为 .
| 3 |
| 3 |
考点:解直角三角形
专题:分类讨论
分析:分四种情况进行讨论:①如图1所示,点P在∠AOB内;②如图2所示,点P在∠AOB外;③如图3所示,点P在∠AOB对顶角的内部;④如图4所示,点P在∠AOB外.
解答:解:分四种情况:
①如图1所示,延长MP交OB于点C.
在Rt△OCM中,∵∠AOB=60°,
∴∠MCO=30°.
在Rt△PCN中,PC=2PN=2
,NC=
=3,
∴MC=4
,OC=
=8,
∴ON=OC-NC=8-3=5;
②如图2所示,由条件可知∠PON=30°,
∴PO=2PN=2
.
∴点C与点M重合,即点M与点O重合.
即ON=PN•tan60°=3;
③如图3,情况与图1完全相同;
④如图4,情况与图2也完全相同.
综上所述,ON的长为5或3.
故答案为:5或3.

①如图1所示,延长MP交OB于点C.
在Rt△OCM中,∵∠AOB=60°,
∴∠MCO=30°.
在Rt△PCN中,PC=2PN=2
| 3 |
| PN |
| tan30° |
∴MC=4
| 3 |
| MC |
| sin60° |
∴ON=OC-NC=8-3=5;
②如图2所示,由条件可知∠PON=30°,
∴PO=2PN=2
| 3 |
∴点C与点M重合,即点M与点O重合.
即ON=PN•tan60°=3;
③如图3,情况与图1完全相同;
④如图4,情况与图2也完全相同.
综上所述,ON的长为5或3.
故答案为:5或3.
点评:本题考查了解直角三角形,难度适中.运用分类讨论与数形结合是解题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
下列说法正确的是( )
| A、正数和负数统称为有理数 |
| B、互为相反数的两数之和为0 |
| C、零是最小的整数 |
| D、若两个数的绝对值相等,则这两个数必相等 |
圆柱和圆锥的底面积、体积分别相等,圆锥的高是圆柱的高的( )
A、
| ||
B、
| ||
| C、2倍 | ||
| D、3倍 |
下列说法正确的是( )
| A、三角形的角平分线是射线 |
| B、过三角形的顶点,且过对边中点的直线是三角形的一条中线 |
| C、一个三角形同一边上的中线、高及这条边所对的角的平分线中,高最短 |
| D、三角形的高、中线、角平分线一定在三角形的内部 |
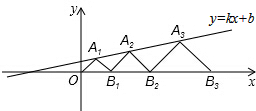 在平面直角坐标系xOy中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=kx+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2(
在平面直角坐标系xOy中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=kx+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2( 如图,正方形ABCD的对角线AC的长为8厘米,则正方形ABCD面积为
如图,正方形ABCD的对角线AC的长为8厘米,则正方形ABCD面积为 解不等式组:
解不等式组: