Question

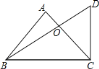
【题目】一副三角板如图所示放置，则的值为________．

Answer 1

【答案】

【解析】

根据题意得出各角的度数，进而利用锐角三角函数关系得出DF，FC，AO，AB，FO的长，进而表示出两三角形面积求出即可．

∵一副三角板如图所示放置，

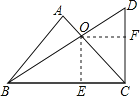
∴过点O作OE⊥BC于点E，作OF⊥DC于点F，

∵∠ACB=45°，∠BCD=90°，

∴∠ACB=∠ACD=45°，∠D=60°，∠DBC=30°，

∴EO=EC=FO=FC，

设EO=EC=FO=FC=x，

∴DF=FOtan60°=x，

CO=x，BE=x，

∴AB=（x+x）=，

故AO==，

∴S△ABO=×AO×AB=××=x2，

S△DOC=×FO×CD=x（x+x）=×x2，

∴S△ODC：S△AOB的值为：×x2：x2=．

故答案为：．