题目内容
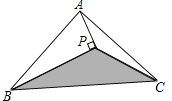
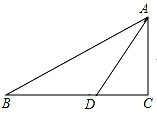
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若动点
,若动点![]() 从点
从点![]() 开始,按
开始,按![]() 的路径运动,且速度为每秒
的路径运动,且速度为每秒![]() ,设出发的时间为
,设出发的时间为![]() 秒.
秒.

(1)出发2秒后,求![]() 的周长.
的周长.
(2)问![]() 为何值时,
为何值时,![]() 为等腰三角形?
为等腰三角形?
(3)另有一点![]() ,从点
,从点![]() 开始,按
开始,按![]() 的路径运动,且速度为每秒
的路径运动,且速度为每秒![]() ,若
,若![]() 、
、![]() 两点同时出发,当
两点同时出发,当![]() 、
、![]() 中有一点到达终点时,另一点也停止运动.当
中有一点到达终点时,另一点也停止运动.当![]() 为何值时,直线
为何值时,直线![]() 把
把![]() 的周长分成
的周长分成![]() 的两部分?
的两部分?
【答案】(1)![]() cm;(2)当
cm;(2)当![]() 为3秒、5.4秒、6秒、6.5秒时,
为3秒、5.4秒、6秒、6.5秒时,![]() 为等腰三角形;(3)
为等腰三角形;(3)![]() 或
或![]() 或
或![]() 秒
秒
【解析】
(1)根据速度为每秒1cm,求出出发2秒后CP的长,然后就知AP的长,利用勾股定理求得PB的长,最后即可求得周长;
(2)分点P在边AC上和点P在边AB上两种情况求解即可;
(3)分类讨论:①当![]() 点在
点在![]() 上,
上,![]() 在
在![]() 上;②当
上;②当![]() 点在
点在![]() 上,
上,![]() 在
在![]() 上;③当
上;③当![]() 点在
点在![]() 上,
上,![]() 在
在![]() 上.
上.
解:(1)如图1,由![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
动点![]() 从点
从点![]() 开始,按
开始,按![]() 的路径运动,且速度为每秒
的路径运动,且速度为每秒![]() ,
,
∴出发2秒后,则![]() ,
,
∴AP=2,
∵![]() ,
,
∴![]() ,
,
∴![]() 的周长为:
的周长为:![]() .
.
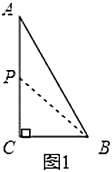
(2)①如图2,若![]() 在边
在边![]() 上时,
上时,![]() ,
,
此时用的时间为![]() ,
,![]() 为等腰三角形;
为等腰三角形;
②2若![]() 在
在![]() 边上时,有三种情况:
边上时,有三种情况:
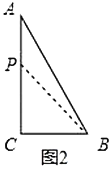
(ⅰ)如图3,若使![]() ,此时
,此时![]() ,
,![]() 运动的路程为
运动的路程为![]() ,
,
所以用的时间为![]() ,
,![]() 为等腰三角形;
为等腰三角形;
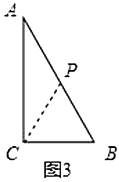
(ⅱ)如图4,若![]() ,作
,作![]() 于点
于点![]() ,
,
∵![]() ,
,
∴CD=![]() ,
,
在![]() 中,
中,
![]() ,
,
所以![]() ,
,
所以![]() 运动的路程为
运动的路程为![]() ,
,
则用的时间为![]() ,
,![]() 为等腰三角形;
为等腰三角形;
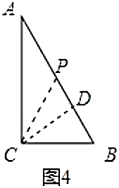
(ⅲ)如图5,若![]() ,此时
,此时![]() 应该为斜边
应该为斜边![]() 的中点,
的中点,![]() 运动的路程为
运动的路程为![]() ,
,
则所用的时间为![]() ,
,![]() 为等腰三角形;
为等腰三角形;
综上所述,当![]() 为
为![]() 、
、![]() 、
、![]() 、
、![]() 时,
时,![]() 为等腰三角形;
为等腰三角形;
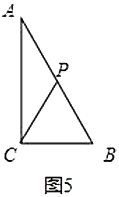
(3)①3÷2=1.5秒,如图6,当![]() 点在
点在![]() 上,
上,![]() 在
在![]() 上,则
上,则![]() ,
,![]() ,
,
∵直线![]() 把
把![]() 的周长分成
的周长分成![]() 的两部分,
的两部分,
∴![]() ,∴
,∴![]() ,符合题意;
,符合题意;
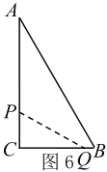
②(3+5) ÷2=4秒,如图7,当![]() 点在
点在![]() 上,
上,![]() 在
在![]() 上,则
上,则![]() ,
,![]() ,
,
∵直线![]() 把
把![]() 的周长分成
的周长分成![]() 的两部分,
的两部分,
∴![]() ,
,![]() ,符合题意;
,符合题意;
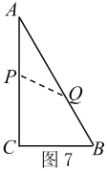
③12÷2=6秒,当![]() 点在
点在![]() 上,
上,![]() 在
在![]() 上,则
上,则![]() ,
,![]() ,
,
∵直线![]() 把
把![]() 的周长分成
的周长分成![]() 的两部分,
的两部分,
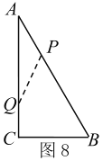
(ⅰ)当AP+AQ=周长的![]() 时,如图8,
时,如图8,
∴![]() ,
,![]() ,符合题意;
,符合题意;
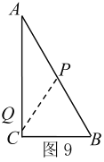
(ⅱ)当AP+AQ=周长的![]() 时,如图9,
时,如图9,
∴![]() ,∴
,∴![]() ;
;
∵当![]() 秒时,点
秒时,点![]() 到达
到达![]() 点停止运动,
点停止运动,
∴![]() 这种情况应该舍去.
这种情况应该舍去.
综上,当![]() 为
为![]() 或
或![]() 或
或![]() 秒时,直线
秒时,直线![]() 把
把![]() 的周长分成
的周长分成![]() 的两部分.
的两部分.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案