题目内容
7．观察下列各等式：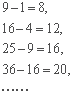
这些等式反映出自然数间的某种规律，设n为自然数，试用关于n的等式表示出你所发现的规律：（n+2）2-n2=4（n+1）．
分析 先将等式进行整理，仔细观察分析整理后的等式不难发现存在的规律，用关于n的等式表示出来即可．
解答 解：将等式进行整理得：
32-12=4（1+1）；
42-22=4（2+1）；
52-32=4（3+1）；
…
所以规律为：（n+2）2-n2=4（n+1），
故答案为：（n+2）2-n2=4（n+1）．
点评 此题主要考查学生对规律型题的掌握情况，做此题注意先对原来的等式进行整理．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
7．
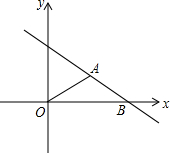如图，在平面直角坐标系中，△ABO为底角是30°的等腰三角形，OA=AB=4，O为坐标原点，点B在x轴上，点P在直线AB上运动，当线段OP最短时PB的长为（ ）
如图，在平面直角坐标系中，△ABO为底角是30°的等腰三角形，OA=AB=4，O为坐标原点，点B在x轴上，点P在直线AB上运动，当线段OP最短时PB的长为（ ）| A． | 2 | B． | 2$\sqrt{3}$ | C． | 4 | D． | 6 |
5．若a-b＞a，a+b＞b，则有（ ）
| A． | ab＜0 | B． | $\frac{a}{b}$＞0 | C． | a+b＞0 | D． | a-b＜0 |
12．
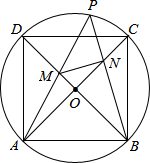如图，正方形ABCD内接于⊙O，P为劣弧$\widehat{CD}$上一点，PA交BD于点M，PB交AC于点N，记∠PBD=θ．若MN⊥PB，则2cos2θ-tanθ的值（ ）
如图，正方形ABCD内接于⊙O，P为劣弧$\widehat{CD}$上一点，PA交BD于点M，PB交AC于点N，记∠PBD=θ．若MN⊥PB，则2cos2θ-tanθ的值（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{2}}}{4}$ |
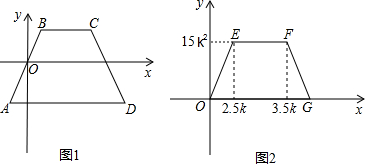
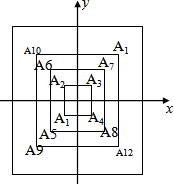如图，所有正方形的中心均在坐标原点，且各边与x轴或y轴平行．从内到外，它们的边长依次为2，4，6，8，…，顶点依次用 A1，A2，A3，A4，…表示，则顶点A2013的坐标是（-504，-504）．
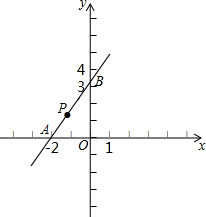如图，直线y=$\sqrt{3}$x+2$\sqrt{3}$与x轴交于点A，与y轴交于点B，动点P从点A开始沿折线AB-BO以1cm/s的速度运动到点O．设点P运动的时间为t（s），△PAO面积为S（cm2）．（坐标轴的单位长度为cm）