题目内容
1. 如图,△ABC中,OB、OC分别平分∠ABC、∠ACB,DE过点O且DE∥BC,已知AB=6,AC=5,BC=7,则△ADE周长为11.
如图,△ABC中,OB、OC分别平分∠ABC、∠ACB,DE过点O且DE∥BC,已知AB=6,AC=5,BC=7,则△ADE周长为11.
分析 根据角平分线的定义可得∠ABO=∠CBO,根据两直线平行,内错角相等可得∠CBO=∠BOD,从而得到∠ABO=∠BOD,再根据等角对等边可得OD=BD,同理可得OE=CE,然后求出△ADE的周长=AB+AC.
解答 解:∵OB平分∠ABC,
∴∠ABO=∠CBO,
∵DE∥BC,
∴∠CBO=∠BOD,
∴∠ABO=∠BOD,
∴OD=BD,
同理可得OE=CE,
∴△ADE的周长=AD+OD+OE+AE=AD+BD+CE+AE=AB+AC,
∵AB=6,AC=5,
∴△ADE周长=6+5=11.
故答案为:11.
点评 本题考查了等腰三角形的判定与性质,角平分线的定义,平行线的性质,熟练掌握各性质是解题的关键.

练习册系列答案
相关题目
9.下列计算正确的是( )
| A. | 23=6 | B. | -42=-16 | C. | -5-2=-3 | D. | -8÷(-2)=-4 |
16.某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
①这批样品的平均质量比标准质量多还是少?用你学过的方法合理解释;
②若标准质量为450克,则抽样检测的总质量是多少?
| 与标准质量的差值(单位:克) | -5 | -2 | 0 | 1 | 3 | 4 |
| 袋数 | 2 | 4 | 5 | 4 | 3 | 2 |
②若标准质量为450克,则抽样检测的总质量是多少?
6.和点P(-3,2)关于x轴对称的点是( )
| A. | (3,2) | B. | (-3,2) | C. | (-3,-2) | D. | (3,-2) |
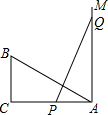 如图所示,有一个直角△ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A垂直于AC的射线AM上运动,当AP=5时,才能使△ABC≌△QPA.
如图所示,有一个直角△ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A垂直于AC的射线AM上运动,当AP=5时,才能使△ABC≌△QPA.