题目内容
11. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=2,CD=4.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=2,CD=4.(1)求证:∠A=∠BCD;
(2)求tanA的值;
(3)求BD的长.
分析 (1)根据余角的性质即可得到结论;
(2)根据三角函数的定义即可得到结论;
(3)根据等角的三角函数值相等即可得到结论.
解答 解:(1)∵∠ACB=90°,CD⊥AB于点D,
∴∠A+∠ACD=∠ACD+∠BCD=90°,
∴∠A=∠BCD;
(2)∵∠ADC=90°,AD=2,CD=4,
∴tanA=$\frac{CD}{AD}$=$\frac{4}{2}$=2;
(3)∵∠A=∠BCD,
∴tan∠BCD=tanA=$\frac{CD}{BD}$=2,
∴BD=8.
点评 本题考查了直角三角形的性质,余角的性质,三角函数的定义,熟记三角函数的定义是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
19.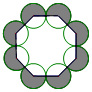 如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(有阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(有阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
 如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(有阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(有阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | 1 |
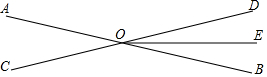 如图,直线AB,CD相交于点O,OE平分∠BOD;若∠AOD:∠BOE=8:1,求∠AOC的度数.
如图,直线AB,CD相交于点O,OE平分∠BOD;若∠AOD:∠BOE=8:1,求∠AOC的度数.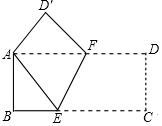 按如图方式折叠长方形纸片ABCD,使顶点A、C重合(图中点D落在点D′处,E,F分别是折痕与BC,AD的交点),已知AB=3,BC=9,求BE及折痕EF的长.
按如图方式折叠长方形纸片ABCD,使顶点A、C重合(图中点D落在点D′处,E,F分别是折痕与BC,AD的交点),已知AB=3,BC=9,求BE及折痕EF的长.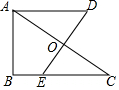 如图,Rt△ABC,∠B=90°,AC的垂直平分线交BC于点E,垂足为点O,过点A作BC的平行线,与直线OE交于点D,若AB=4,BC=6,则AD的长为$\frac{13}{3}$.
如图,Rt△ABC,∠B=90°,AC的垂直平分线交BC于点E,垂足为点O,过点A作BC的平行线,与直线OE交于点D,若AB=4,BC=6,则AD的长为$\frac{13}{3}$. 如图,AO⊥BC,垂足为O,且∠COD-∠AOD=34°28′.求∠BOD的度数.
如图,AO⊥BC,垂足为O,且∠COD-∠AOD=34°28′.求∠BOD的度数.