题目内容
3.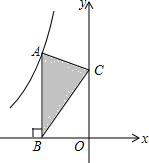 如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,过点A作AB⊥x轴,垂足为B,点C为y轴上的一点,连接AC、BC,若△ABC的面积为3,则k的值是-6.
如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,过点A作AB⊥x轴,垂足为B,点C为y轴上的一点,连接AC、BC,若△ABC的面积为3,则k的值是-6.
分析 连结OA,如图,利用三角形面积公式得到S△OAB=S△CAB=3,再根据反比例函数的比例系数k的几何意义得到$\frac{1}{2}$|k|=3,然后去绝对值即可得到满足条件的k的值.
解答 解:连结OA,如图,
∵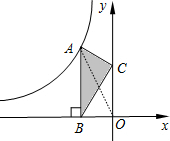 AB⊥x轴,
AB⊥x轴,
∴OC∥AB,
∴S△OAB=S△CAB=3,
而S△OAB=$\frac{1}{2}$|k|,
∴$\frac{1}{2}$|k|=3,
∵k<0,
∴k=-6.
故答案为:-6.
点评 本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.

练习册系列答案
相关题目
13. 如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
 如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )| A. | 2.4cm | B. | 4.8cm | C. | 5cm | D. | 9.6cm |
11. 如图,已知a∥b,将一块三角尺放在这两条直线之间,使直角顶点在直线a上,较小的锐角的顶点在直线b上.若∠1=25°,则∠2的度数为( )
如图,已知a∥b,将一块三角尺放在这两条直线之间,使直角顶点在直线a上,较小的锐角的顶点在直线b上.若∠1=25°,则∠2的度数为( )
 如图,已知a∥b,将一块三角尺放在这两条直线之间,使直角顶点在直线a上,较小的锐角的顶点在直线b上.若∠1=25°,则∠2的度数为( )
如图,已知a∥b,将一块三角尺放在这两条直线之间,使直角顶点在直线a上,较小的锐角的顶点在直线b上.若∠1=25°,则∠2的度数为( )| A. | 25° | B. | 35° | C. | 55° | D. | 65° |
8.从青岛到济南有南线和北线两条高速公路,南线全长400千米,北线全长320千米.甲、乙两辆客车分别有南线和北线从青岛同时驶往济南,已知客车甲在南线高速公路上行驶的平均速度比客车乙在北线高速公路上快20千米/小时,两车恰好同时到达济南.若设客车乙从青岛到济南的平均速度是x千米/小时,则根据题意可得方程( )
| A. | $\frac{400}{x-20}$=$\frac{320}{x}$ | B. | $\frac{400}{x+20}$=$\frac{320}{x}$ | C. | $\frac{400}{x}$+20=$\frac{320}{x}$ | D. | $\frac{400}{x}$=$\frac{320}{x+20}$ |
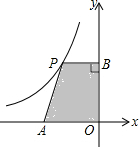 如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数$y=-\frac{4}{x}$(x<0)上一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数$y=-\frac{4}{x}$(x<0)上一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( ) 如图所示的几何体是由一些小正方体组合而成的,若每个小正方体的棱长都是1,则该几何体俯视图的面积是5.
如图所示的几何体是由一些小正方体组合而成的,若每个小正方体的棱长都是1,则该几何体俯视图的面积是5.