题目内容
5.解方程组:(1)$\left\{\begin{array}{l}{2x+5y=8}\\{3x+2y=5}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2x+3y=6}\\{3x-2y=-2}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{2x+5y=8①}\\{3x+2y=5②}\end{array}\right.$,
①×3-②×2得:11y=14,即y=$\frac{14}{11}$,
把y=$\frac{14}{11}$代入①得:x=$\frac{9}{11}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{9}{11}}\\{y=\frac{14}{11}}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2x+3y=6①}\\{3x-2y=-2②}\end{array}\right.$,
①×2+②×3得:13x=6,即x=$\frac{6}{13}$,
把x=$\frac{6}{13}$代入①得:y=$\frac{22}{13}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{6}{13}}\\{y=\frac{22}{13}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对角线交点O处,折痕为EF,若菱形ABCD的边长为2cm,∠B=60°,那么EF=$\sqrt{3}$cm.
如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对角线交点O处,折痕为EF,若菱形ABCD的边长为2cm,∠B=60°,那么EF=$\sqrt{3}$cm. 如图,矩形ABCD的对角线相交于O,BE⊥DE,OF⊥DF,求证:点F是DE的中点.
如图,矩形ABCD的对角线相交于O,BE⊥DE,OF⊥DF,求证:点F是DE的中点.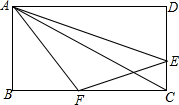 如图,在矩形ABCD中,AB=3cm,AD=6cm,点E从点C开始沿边CD以1cm/s的速度向点D移动,点F从点B开始沿边BC以2cm/s的速度向点C移动,如果EF同时出发,用t(s)表示移动的时间(0≤t≤3).当t为何值时,以A,B,F为顶点的三角形与以E,F,C为顶点的三角形相似?
如图,在矩形ABCD中,AB=3cm,AD=6cm,点E从点C开始沿边CD以1cm/s的速度向点D移动,点F从点B开始沿边BC以2cm/s的速度向点C移动,如果EF同时出发,用t(s)表示移动的时间(0≤t≤3).当t为何值时,以A,B,F为顶点的三角形与以E,F,C为顶点的三角形相似?