��Ŀ����
����ͼ1��ֱ��y=2x�뷴��������y=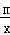 ��ͼ���ڵ�A��3��n������B���߶�OA�ϵ�һ�����㣮
��ͼ���ڵ�A��3��n������B���߶�OA�ϵ�һ�����㣮
��1����m=18��OA=3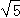 ��
��
��2�������ǰ��ֱ�Ƕ�������ڵ�B�������� �������ֱ�DZ߷ֱ�x�ᡢy����C��D���㣬��
�������ֱ�DZ߷ֱ�x�ᡢy����C��D���㣬��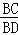 ��ֵ��
��ֵ��
��3����ͼ2��B���߶�OA���е㣬E�ڷ�����������ͼ���ϣ���̽������x�����Ƿ���ڵ�F��ʹ�á�EAB=��EBF=��AOF��������ڣ��������F�����ꣻ��������ڣ���˵�����ɣ�
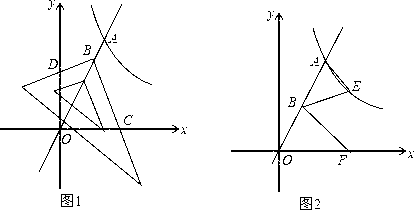
�����㡿�����������ۺ��⣮
��ר�⡿�ۺ��⣮
����������1���Ȱ�A��3��n������y=2x���n���Ӷ��õ�A��3��6���������������ľ��빫ʽ�����OA=3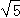 ��Ȼ����ݷ���������ͼ���ϵ������������m=18��
��Ȼ����ݷ���������ͼ���ϵ������������m=18��
��2����B�ֱ���x���y��Ĵ��ߣ�����ֱ�ΪM��N����ͼ1����B��a��2a������BM=2a��BN=a�����õȽǵ������ȵõ���MBC=��DBN�����ǿ��ж�Rt��MBC��Rt��DBN��Ȼ���������Ʊ���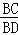 =2��
=2��
��3����AH��y����H���ӳ�AE��x����G�㣬����GB����ͼ2���ɡ�EAB=��AOF�õ���GAOΪ���������Σ��ٸ��ݵ��������ε����ʵ�GB��OA������֤��Rt��OBG��Rt��AHO���������Ʊȼ����OG= ���õ�G��
���õ�G�� ��0����Ȼ�����ô���ϵ�������ֱ��AG�Ľ���ʽΪy=��
��0����Ȼ�����ô���ϵ�������ֱ��AG�Ľ���ʽΪy=�� x+10����ͨ���ⷽ����
x+10����ͨ���ⷽ���� ��E������Ϊ��
��E������Ϊ�� ��4�������ǿ����������ľ��빫ʽ�����AE=
��4�������ǿ����������ľ��빫ʽ�����AE= �����֤����ABE�ס�OFB���������Ʊȼ����OF���Ӷ��õ�F������꣮
�����֤����ABE�ס�OFB���������Ʊȼ����OF���Ӷ��õ�F������꣮
����𡿽⣺��1����A��3��n������y=2x��n=2��3=6����A��3��6����
����OA= =3
=3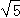 ��
��
����A�ڷ���������y=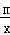 ͼ���ϣ�
ͼ���ϣ�
����m=3��6=18��
�ʴ� ��Ϊ18��3
��Ϊ18��3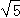 ��
��
��2����B�ֱ���x���y��Ĵ��ߣ�����ֱ�ΪM��N����ͼ1����B��a��2a������BM=2a��BN=a��
�ߡ�MBC+��MBD=90�㣬��DBN+��MBD=90�㣬
���MBC=��DBN��
��Rt��MBC��Rt��DBN��
��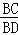 =
= =
= =2��
=2��
��3�����ڣ�
��AH��y����H���ӳ�AE��x����G�㣬����GB����ͼ2��
�ߡ�EAB=��AOF��
���GAO����������
��B���߶�OA���е㣬
��GB��OA��
��AH��x�ᣬ
���OAH=��GOB��
��Rt��OBG��Rt��AHO��
�� =
= ����
���� =
= �����OG=
�����OG=
��G�� ��0����
��0����
��ֱ��AG�Ľ���ʽΪy=kx+b��
��A��3��6����G�� ��0�������
��0������� ��
��
��� ��
��
��ֱ��AG�Ľ���ʽΪy=�� x+10��
x+10��
�ⷽ���� ��
�� ��
�� ��
��
��E�������� ��4����
��4����
��AE= =
= ��
��
�ߡ�EBO=��EAB+��2������1+��EBF=��EAB+��2��
����EAB=��EBF��
���1=��2��
�ߡ�EAB=��BOF��
���ABE�ס�OFB��
�� =
= ����
���� =
= ��
��
��OF= ��
��
��F��������� ��0����
��0����


�����������⿼���˷����������ۺ��⣺�������շ���������ͼ���ϵ������������һ�κ���ͼ���ϵ����������������������ͼ�����ʣ������������ľ��빫ʽ�����߶εij������������������ε��ж������ʼ����߶εij��ȣ�

 B��
B�� C��
C�� D��
D��

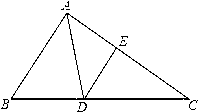

 ��ϵ����__________��
��ϵ����__________��