题目内容
如图,正方形ABCD中,CD=5,BE=CF,且DG2+GE2=28,则AE的长______.


【考点】正方形的性质;全等三角形的判定与性质;勾股定理.
【分析】连接DE,由正方形的性质得出AB=BC=CD=DA=5,∠A=∠BCD=∠B=90°,由SAS证明△BCE≌△CDF,得出对应角相等∠BEC=∠CFD,再由角的互余关系证出△DGE是直角三角形,由勾股定理求出DE2,AE2,即可得出AE的长.
【解答】解:连接DE,如图所示:
∵四边形ABCD是正方形,
∴AB=BC=CD=DA=5,∠A=∠BCD=∠B=90°,
在△BCE和△CDF中,
 ,
,
∴△BCE≌△CDF(SAS),
∴∠BEC=∠CFD,
∵∠BEC+∠BCE=90°,
∴∠CFD+∠BCE=90°,
∴∠DGE=∠CGF=90°,
∴DE2=DG2+GE2=28,
∴AE2=DE2﹣AD2=28﹣25=3,
∴AE= ;
;
故答案为: .
.


练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 =k成立,那么k的值为( )
=k成立,那么k的值为( ) A.1 B.-2 C.-2或1 D.以上都不对
A.1 B.-2 C.-2或1 D.以上都不对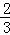 ,12,﹣(﹣96),﹣|﹣3|,﹣4.5,0,|﹣2.5|,
,12,﹣(﹣96),﹣|﹣3|,﹣4.5,0,|﹣2.5|,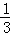
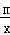 的图象交于点A(3,n),点B是线段OA上的一个动点.
的图象交于点A(3,n),点B是线段OA上的一个动点.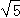 ;
; 板的两条直角边分别交x轴、y轴于C、D两点,求
板的两条直角边分别交x轴、y轴于C、D两点,求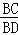 的值;
的值;