题目内容
小乐发明了一个魔术盒,当任意有理数对(a,b)放入盒中时,会得到一个新的有理数:a3+3a2b+3ab2+b3.
例如把(3,-2)放入其中,就会得到33+3×32×(-2)+3×3×(-2)2+(-2)3=19-18=1.
(1)现将有理数对(-2,3)放入盒中得到有理数m,再将有理数对(m,-7)放入盒中后,得到的有理数是多少?有一位有思考的老师给我提出了这样的修改建议很好,先谢他了!七年级最后一题他认为难度不够,建议修改如下:
(2)小乐先放入有理数对(2014,-2015),如果再放入有理数对(-2015,2014),那么两次得到的有理数会相等吗?请你说明理由.
(3)在(2)中,你还能放入有理数对(-2013, ),( ,2013)使得得到的有理数也和得到的有理数相等.
(4)小乐先放入有理数对(m,n),请你放入有理数对( , ),让得到有理数与小乐得到有理数相等.
例如把(3,-2)放入其中,就会得到33+3×32×(-2)+3×3×(-2)2+(-2)3=19-18=1.
(1)现将有理数对(-2,3)放入盒中得到有理数m,再将有理数对(m,-7)放入盒中后,得到的有理数是多少?有一位有思考的老师给我提出了这样的修改建议很好,先谢他了!七年级最后一题他认为难度不够,建议修改如下:
(2)小乐先放入有理数对(2014,-2015),如果再放入有理数对(-2015,2014),那么两次得到的有理数会相等吗?请你说明理由.
(3)在(2)中,你还能放入有理数对(-2013,
(4)小乐先放入有理数对(m,n),请你放入有理数对(
考点:有理数的混合运算
专题:新定义
分析:(1)根据运算的规定代入(-2,3)得到m,再进一步代入(m,-7)得出结果即可;
(2)代入有理数对(2014,-2015)和(-2015,2014),进行计算验证即可;
(3)类比(2)的方法,代入得有理数对的两个数的和相等即可;
(4)利用(3)的结论得出结果.
(2)代入有理数对(2014,-2015)和(-2015,2014),进行计算验证即可;
(3)类比(2)的方法,代入得有理数对的两个数的和相等即可;
(4)利用(3)的结论得出结果.
解答:解:(1)依题意可得:m=(-2)3+3×(-2)2×3+3×(-2)×32+33=-8+36-54+27=1,
最终的有理数为:13+3×12×(-7)+3×1×(-7)2+(-7)3=-20+147-343=-216;
(2)有理数对(2014,-2015)为:20143+3×20142×(-2015)+3×2014×(-2015)2+(-2015)3=20143-3×20142×2015+3×2014×20152-20153
有理数对(-2015,2014)为:(-2015)3+3×(-2015)2×2014+3×(-2015)×20142+20143
=-20153+3×2014×20152-3×20142×2015+20143=20143-3×20142×2015+3×2014×20152-20153
∴小乐先放入有理数对(2014,-2015),如果再放入有理数对(-2015,2014),那么两次得到的有理数相等;
(3)∵a3+3a2b+3ab2+b3=(a+b)3,
∴只要代入有理数对的两个数的和相等即可,
-2013+2012=-2014+2013=-1;
(4)小乐先放入有理数对(m,n),和为m+n;放入有理数对(n,m),得到有理数与小乐得到有理数相等.
最终的有理数为:13+3×12×(-7)+3×1×(-7)2+(-7)3=-20+147-343=-216;
(2)有理数对(2014,-2015)为:20143+3×20142×(-2015)+3×2014×(-2015)2+(-2015)3=20143-3×20142×2015+3×2014×20152-20153
有理数对(-2015,2014)为:(-2015)3+3×(-2015)2×2014+3×(-2015)×20142+20143
=-20153+3×2014×20152-3×20142×2015+20143=20143-3×20142×2015+3×2014×20152-20153
∴小乐先放入有理数对(2014,-2015),如果再放入有理数对(-2015,2014),那么两次得到的有理数相等;
(3)∵a3+3a2b+3ab2+b3=(a+b)3,
∴只要代入有理数对的两个数的和相等即可,
-2013+2012=-2014+2013=-1;
(4)小乐先放入有理数对(m,n),和为m+n;放入有理数对(n,m),得到有理数与小乐得到有理数相等.
点评:此题考查有理数的混合运算,关键是找出运算的规律,解决问题.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
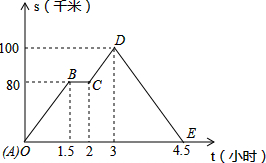 如图:图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,回答:
如图:图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,回答: 李华晚上在两站相距50m的路灯下来回散步,DF=50m.已知李华身高AB=1.7m,灯柱CD=EF=8.5m.
李华晚上在两站相距50m的路灯下来回散步,DF=50m.已知李华身高AB=1.7m,灯柱CD=EF=8.5m.