题目内容
李华晚上在两站相距50m的路灯下来回散步，DF=50m．已知李华身高AB=1.7m，灯柱CD=EF=8.5m．（1）若李华距灯柱CD的距离为DB=xm，他的影子BQ=ym，求y关于x的函数关系式．
（2）若李华在两路灯之间行走，则他前后两个影子PB+BQ是否会发生变化？请说明理由．
考点：相似三角形的应用,中心投影
专题：
分析：（1）易证△QAB∽△QCD，根据相似三角形的对应边的比相等就可以得到x，y的一个关系式，从而求出函数的解析式．
（2）在两个路灯之间行走时影长之和为定值．
（2）在两个路灯之间行走时影长之和为定值．
解答：解：（1）∵CD∥AB，
∴△QAB∽△QCD．
∴
=
，
∵DB=xm，他的影子BQ=ym，AB=1.7米，CD=8.5米，
∴
=
整理得：y=
；
（2）由（1）可得BQ=
，
同理可得PB=
，
则PB+BQ=
+
=
=12.5，是定值．
∴△QAB∽△QCD．
∴
| QB |
| QD |
| AB |
| CD |
∵DB=xm，他的影子BQ=ym，AB=1.7米，CD=8.5米，
∴
| y |
| x+y |
| 1.7 |
| 8.5 |
整理得：y=
| x |
| 4 |
（2）由（1）可得BQ=
| DB |
| 4 |
同理可得PB=
| BF |
| 4 |
则PB+BQ=
| DB |
| 4 |
| BF |
| 4 |
| DF |
| 4 |
点评：考查相似三角形的应用；用到的知识点为：平行于三角形一边的直线与三角形另两边相交，截得的两三角形相似；相似三角形的对应边成比例．
练习册系列答案
相关题目
中国载人航天工程新闻发言人武平在国务院新闻办2012年6月24日举行的新闻发布会上介绍，我国从1992年实施载人航天工程到神舟九号任务完成投入经费将达到三百九十亿元左右．其中三百九十亿用科学记数法表示为（ ）
| A、3.9×1010 |
| B、0.39×1012 |
| C、3.9×1011 |
| D、3.9×1012 |
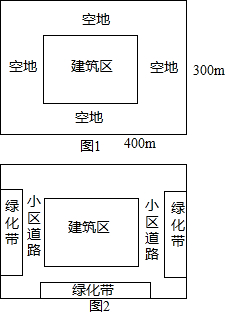如图1，某小区的平面图是一个占地400×300平方米的矩形，正中央的建筑区是与整个小区长宽比例相同的矩形．如果要使四周的空地所占面积是小区面积的36%，南北空地等宽，东西空地等宽．
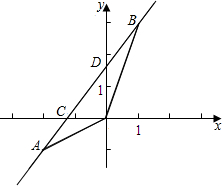如图，已知一次函数y=kx+b的图象经过A（-2，-1），B（1，3）两点，并且交x轴于点C，交y轴于点D．