题目内容
14．把下列多项式分解因式：（1）-2x3+18x；
（2）（a+2b）2+2（a+2b-1）+3．
分析 （1）直接提取公因式-2x，进而利用平方差公式分解因式得出答案；
（2）直接去括号，再利用完全平方公式分解因式得出答案．
解答 解：（1）-2x3+18x
=-2x（x2-9）
=-2x（x+3）（x-3）；
（2）（a+2b）2+2（a+2b-1）+3
=（a+2b）2+2（a+2b）+1
=（a+2b+1）2．
点评 此题主要考查了提取公因式法以及公式法分解因式，正确应用乘法公式是解题关键．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
4．已知：x=$\sqrt{2+\sqrt{3}}$，y=$\sqrt{2-\sqrt{3}}$，则代数式x+y的值为（ ）
| A． | 4 | B． | 2$\sqrt{3}$ | C． | $\sqrt{6}$ | D． | $\sqrt{2}$ |
5．下列说法错误的是（ ）
| A． | $\sqrt{3}$是3的平方根 | B． | |$\sqrt{2}$-1|=$\sqrt{2}$-1 | ||
| C． | -$\sqrt{5}$的相反数是$\sqrt{5}$ | D． | 带根号的数都是无理数 |
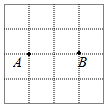如图4×4的正方形网格每个小正方形的边长为1，每个小正方形的顶点叫格点，点A，B（均在格点上）的位置如图，若以A，B为顶点画面积为2的格点平行四边形，则符合条件的平行四边形的个数有（ ）
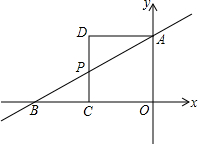如图，在直角坐标系中，直线AB分别与x轴、y轴交于B、A两点，OA、OB的长是关于x的一元二次方程x2-12x+32=0的两个实数根，且OB＞OA，以OA为一边作如图所示的正方形AOCD，CD交AB于点P．