Question

一次函数y=

1

3

x+2和y=-

1

2

x+2与x轴分别交于A，B两点，且与y轴交于同一点C，则△ABC的面积是

 

．

Answer 1

分析：先根据两函数与x轴有交点时y=0，确定x的值即得AB点的坐标，再根据与y轴交于同点，确定C点的坐标，根据三点的坐标求△ABC的面积．

解答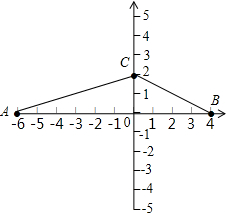：解：∵一次函数y=

1

3

x+2和y=-

1

2

x+2与x轴分别交于A，B两点，
∴

1

3

x+2=0，-

1

2

x+2=0，
解得A点的坐标为（-6，0），B点的坐标为（4，0）；
∵两个函数与y轴交于同一点C，
∴C点的坐标为（0，2），
如图所示，
∴△ABC的面积=

1

2

×10×2=10．
故填10．

点评：本题考查了二元一次方程组的解法，涉及到点的坐标、三角形的面积等知识点，是一道考查学生综合知识运用能力的好题．