题目内容
12.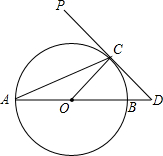 如图,AB是⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且AO=CD,则∠PCA=( )
如图,AB是⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且AO=CD,则∠PCA=( )| A. | 30° | B. | 60° | C. | 67.5° | D. | 45° |
分析 直接利用切线的性质结合等腰三角形的性质得出∠PCA的度数.
解答 解:∵PD切⊙O于点C,
∴∠OCD=90°,
∵AO=CD,
∴OC=DC,
∴∠COD=∠D=45°,
∵AO=CO,
∴∠A=∠ACO=22.5°,
∴∠PCA=90°-22.5°=67.5°.
故选:C.
点评 此题主要考查了切线的性质以及等腰三角形的性质,正确得出∠COD=∠D=45°是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.下列函数中,y随x的增大而减小的是( )
| A. | y=x | B. | y=x2 | C. | y=$\frac{2}{x}$ | D. | y=$\frac{4}{x}$(x<0) |
7. 如图,在圆内接四边形ABCD中,∠B=50°,则∠D=( )
如图,在圆内接四边形ABCD中,∠B=50°,则∠D=( )
 如图,在圆内接四边形ABCD中,∠B=50°,则∠D=( )
如图,在圆内接四边形ABCD中,∠B=50°,则∠D=( )| A. | 40° | B. | 130° | C. | 120° | D. | 150° |
4.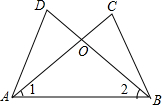 如图,已知∠1=∠2,若用“SAS”来判定△ACB≌△BDA,则还需要添加的一个条件是( )
如图,已知∠1=∠2,若用“SAS”来判定△ACB≌△BDA,则还需要添加的一个条件是( )
 如图,已知∠1=∠2,若用“SAS”来判定△ACB≌△BDA,则还需要添加的一个条件是( )
如图,已知∠1=∠2,若用“SAS”来判定△ACB≌△BDA,则还需要添加的一个条件是( )| A. | AD=BC | B. | AC=BD | C. | ∠C=∠D | D. | OA=OB |
 利用二次函数y=x2-5x+5的图象,探索方程x2-5x+5=0的介于1~2之间的根(精确到0.1).
利用二次函数y=x2-5x+5的图象,探索方程x2-5x+5=0的介于1~2之间的根(精确到0.1). 如图,在长方形纸片ABCD中,AB=6cm,BC=10cm,将长方形纸片沿AE折叠,使点D落在BC边的点F处.试求折痕AE的长.
如图,在长方形纸片ABCD中,AB=6cm,BC=10cm,将长方形纸片沿AE折叠,使点D落在BC边的点F处.试求折痕AE的长.