题目内容
7．
如图，正方形ABCD的周长为28 cm，则矩形MNGC的周长是（ ）| A． | 24cm | B． | 14cm | C． | 18cm | D． | 7cm |
分析 由正方形ABCD的周长为28cm，易得BC+CD=14cm，又由矩形NMCG，易得△BNG与△DNM是等腰直角三角形，继而求得答案．
解答 解：∵四边形ABCD是正方形，
∴∠DBC=∠BDC=45°，
∵正方形ABCD的周长为28cm，
∴BC+CD=14（cm），
∵四边形NMCG是矩形，
∴∠NGB=∠NMD=90°，
∴△BNG与△DNM是等腰直角三角形，
∴BG=GN，NM=DM，
∴矩形MNGC的周长是：MN+MC+CG+NG=BC+CD=14（cm）．
故选B．
点评 本题考查了正方形的性质的运用，矩形的性质的运用及矩形的周长的计算方法的运用．解答本题的关健是找到矩形的周长与正方形的边长之间的关系．
练习册系列答案
黄冈创优卷系列答案
相关题目
13．
今年5月，某大型商业集团随机抽取所属的m家商业连锁店进行评估，将各连锁店按照评估成绩分成了A、B、C、D四个等级，绘制了如图尚不完整的统计图表．
根据以上信息解答下列问题：
（1）求m的值；
（2）在扇形统计图中，求B等级所在扇形的圆心角的大小；（结果用度、分、秒表示）
（3）从评估成绩不少于80分的连锁店中任选2家介绍营销经验，求其中至少有一家是A等级的概率．
今年5月，某大型商业集团随机抽取所属的m家商业连锁店进行评估，将各连锁店按照评估成绩分成了A、B、C、D四个等级，绘制了如图尚不完整的统计图表．| 评估成绩n（分） | 评定等级 | 频数 |
| 90≤n≤100 | A | 2 |
| 80≤n＜90 | B | |
| 70≤n＜80 | C | 15 |
| n＜70 | D | 6 |
（1）求m的值；
（2）在扇形统计图中，求B等级所在扇形的圆心角的大小；（结果用度、分、秒表示）
（3）从评估成绩不少于80分的连锁店中任选2家介绍营销经验，求其中至少有一家是A等级的概率．
10．对部分参加夏令营的中学生的年龄（单位：岁）进行统计，结果如表：
则这些学生年龄的众数是17岁．
| 年龄 | 13 | 14 | 15 | 16 | 17 | 18 |
| 人数 | 4 | 5 | 6 | 6 | 7 | 2 |
2．
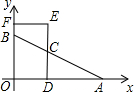如图，在平面直角坐标系中，点A、B的坐标分别为（4，0）、（0，2），点C为线段AB上任意一点（不与点A、B重合），CD⊥OA于点D，点E在DC的延长线上，EF⊥y轴于点F，若点C为DE的中点，则四边形ODEF的周长为（ ）
如图，在平面直角坐标系中，点A、B的坐标分别为（4，0）、（0，2），点C为线段AB上任意一点（不与点A、B重合），CD⊥OA于点D，点E在DC的延长线上，EF⊥y轴于点F，若点C为DE的中点，则四边形ODEF的周长为（ ）| A． | 4 | B． | 6 | C． | 8 | D． | 10 |
19．非零数a的倒数是（ ）
| A． | a | B． | |a| | C． | $\frac{1}{a}$ | D． | -a |
如图，小明在窗台C处，测得大树AB的顶部A的仰角为45°，测得大树AB的底部B的俯角为30°，已知窗台C处离地面的距离CD为5m，则大树的高度为5+5$\sqrt{3}$m．（结果保留根号）
17．将抛物线y=-3x2-1向右平移1个单位长度，再向上平移1个单位长度后所得的抛物线的解析式为（ ）
| A． | y=-3（x-1）2 | B． | y=-3（x+1）2 | C． | y=-3（x-1）2+2 | D． | y=-3（x-1）2-2 |