题目内容
10.选取二次三项式ax2+bx+c(a≠0)中两项,配成完全平方式的过程叫配方,例如①选取二次项和一次项配方:x2-4x+2=(x-2)2-2
②选取二次项和常数项配方:x2-4x+2=(x-$\sqrt{2}$)2+($2\sqrt{2}$-4)x,或x2-4x+2=(x+$\sqrt{2}$)2-($2\sqrt{2}$+4)x
③选取一次项和常数项配方:x2-4x+2=($\sqrt{2}$x-$\sqrt{2}$)2-x2
根据以上材料,解决下面问题:
(1)写出x2-8x+4的两种不同形式的配方;
(2)已知x2+y2+xy-3y+3=0,求xy的值.
分析 (1)根据配方法的步骤根据二次项系数为1,常数项是一次项系数的一半的平方进行配方和二次项和常数项在一起进行配方即可.
(2)根据配方法的步骤把x2+y2+xy-3y+3=0变形为(x+$\frac{1}{2}$y)2+$\frac{3}{4}$(y-2)2=0,再根据x+$\frac{1}{2}$y=0,y-2=0,求出x,y的值,即可得出答案.
解答 解:(1)x2-8x+4
=x2-8x+16-16+4
=(x-4)2-12;
x2-8x+4
=(x-2)2+4x-8x
=(x-2)2-4x;
(2)x2+y2+xy-3y+3=0,
(x+$\frac{1}{2}$y)2+$\frac{3}{4}$(y-2)2=0,
x+$\frac{1}{2}$y=0,y-2=0,
x=-1,y=2,
则xy=(-1)2=1;
点评 本题考查了配方法的应用,根据配方法的步骤和完全平方公式:a2±2ab+b2=(a±b)2进行配方是解题的关键,是一道基础题.

练习册系列答案
相关题目
1.下列说法:①若a、b互为相反数,则a+b=0;②若a+b=0,则a、b互为相反数;③若a、b互为相反数,则$\frac{a}{b}$=-1; ④若$\frac{a}{b}$=-1,则a、b互为相反数.其中正确的结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.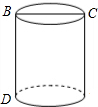 如图,一圆柱体的底面周长为24cm,高BD为5cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的侧面爬行到点C的最短路程大约是( )
如图,一圆柱体的底面周长为24cm,高BD为5cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的侧面爬行到点C的最短路程大约是( )
 如图,一圆柱体的底面周长为24cm,高BD为5cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的侧面爬行到点C的最短路程大约是( )
如图,一圆柱体的底面周长为24cm,高BD为5cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的侧面爬行到点C的最短路程大约是( )| A. | 6cm | B. | 12cm | C. | 13cm | D. | 16cm |
15.下列计算正确的是( )
| A. | -8-3=-5 | B. | 0-(-6)=-6 | C. | -23=-8 | D. | 7÷$\frac{1}{7}$×7=7 |
2.数轴上有一点P表示的数是2,与P点距离3个单位长度的点Q所表示的数是( )
| A. | 5 | B. | -1 | C. | -1或5 | D. | -3 |
 在四边形ABDC中,AB=AC,∠B=∠C,BD=10,则DC=10.
在四边形ABDC中,AB=AC,∠B=∠C,BD=10,则DC=10.