题目内容
 点M是正方形ABCD的边AB的中点,连接DM,将△ADM沿DM翻折得△A′DM,延长MA′交DC的延长线于点E,求
点M是正方形ABCD的边AB的中点,连接DM,将△ADM沿DM翻折得△A′DM,延长MA′交DC的延长线于点E,求| CE |
| DE |
考点:翻折变换(折叠问题)
专题:
分析:设正方形ABCD的边长为2a,CE=x,根据正方形的性质得AD=CD=2a,ME=2a+x,由点M是正方形ABCD的边AB的中点得AM=a,再根据折叠的性质得A'M=AM=a,DA'=DA=2a,∠AMD=∠DMA',∠DA'M=∠A=90°,依据等角对等边,证明ME=MD=2a+x,A'E=ME-MA'=2a+x-a=a+x,在Rt△DA'E中,根据勾股定理得(2a)2+(a+x)2=(2a+x)2,解得a(用x表示),即可求得线段的比.
解答:解:设正方形ABCD的边长为2a,CE=x,则AD=CD=2a,DE=2a+x,
∵点M是正方形ABCD的边AB的中点,
∴AM=a,
∵将△ADM翻折得到△A'DM,
∴MA'=AM=a,DA'=DA=2a,∠AMD=∠DMA',∠DA'M=∠A=90°,
∵AB∥CD,
∴∠AMD=∠MDE,
∴∠DME=∠MDE,
∴ME=DE=2a+x,
∴A'E=ME-MA'=2a+x-a=a+x,
在Rt△EDA'中,
∵DA'2+A'E2=DE2,
∴(2a)2+(a+x)2=(2a+x)2,
∴a=2x,
∴CD=4x,DE=5x.
∴
=
.
∵点M是正方形ABCD的边AB的中点,
∴AM=a,
∵将△ADM翻折得到△A'DM,

∴MA'=AM=a,DA'=DA=2a,∠AMD=∠DMA',∠DA'M=∠A=90°,
∵AB∥CD,
∴∠AMD=∠MDE,
∴∠DME=∠MDE,
∴ME=DE=2a+x,
∴A'E=ME-MA'=2a+x-a=a+x,
在Rt△EDA'中,
∵DA'2+A'E2=DE2,
∴(2a)2+(a+x)2=(2a+x)2,
∴a=2x,
∴CD=4x,DE=5x.
∴
| CE |
| DE |
| 1 |
| 5 |
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了正方形的性质和勾股定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列方程中,解是x=2的方程是( )
| A、3x=x+3 |
| B、-x+3=0 |
| C、5x-2=8 |
| D、2x=6 |
 如图,AF是△ABC的高线,AD、BE分别是△ABC的角平分线,AD、BE交于点O,且∠ABC=36°,∠C=76°.求∠DAF和∠DOE的度数.
如图,AF是△ABC的高线,AD、BE分别是△ABC的角平分线,AD、BE交于点O,且∠ABC=36°,∠C=76°.求∠DAF和∠DOE的度数.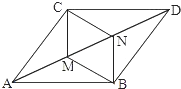 如图,?ABDC中,BN⊥AB,交AD于点N,CM⊥CD,交AD于点M,连接BM、CN
如图,?ABDC中,BN⊥AB,交AD于点N,CM⊥CD,交AD于点M,连接BM、CN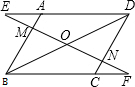 已知:如图在平行四边形ABCD中,对角线BD的中点为O,过点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F.
已知:如图在平行四边形ABCD中,对角线BD的中点为O,过点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F.