题目内容
2.已知a,b,c是实数,且a+b+c=6$\sqrt{a+3}$+8$\sqrt{b+8}$+6$\sqrt{c-1}$-44,求a+b+c的值.分析 已知等式整理,利用完全平方公式变形,再利用非负数的性质求出a,b,c的值,即可求出a+b+c的值.
解答 解:已知等式整理得:(a+3-6$\sqrt{a+3}$+9)+(b+8-8$\sqrt{b+8}$+16)+(c-1-6$\sqrt{c-1}$+9)=0,
即($\sqrt{a+3}$-3)2+($\sqrt{b+8}$-4)2+($\sqrt{c-1}$-3)2=0,
∴$\sqrt{a+3}$=3,$\sqrt{b+8}$=4,$\sqrt{c-1}$=3,
解得:a=6,b=8,c=10,
则a+b+c=6+8+10=24.
点评 此题考查了配方法的应用,以及非负数的性质,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.下列合并同类项中,正确的是( )
| A. | 3x+3y=6xy | B. | 2a2+3a3=5a3 | C. | 3mn-2mn=mn | D. | 7x-5x=2 |
14.某股票经纪人给他的投资者列出下表,说明投资人的盈利净赚情况:(单位:元)
请你计算一下,投资者到底赔了还是赚了?赔或赚了多少元?
| 股票名称 | 每股净赚(元) | 股数 |
| 天河 | +4 | 500 |
| 北斗 | -1.5 | 1000 |
| 白马 | +3 | 1000 |
| 海潮 | -2 | 500 |
8.下列函数中,y随x的增大而减小的有( )
| A. | y=-x | B. | y=2+3x | C. | y=5x | D. | y=-3+2x |
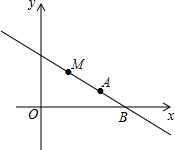 如图,一次函数y=kx+3(k≠0)的图象经过点A(4,1),与x轴相交于点B,直线上有一点M(a,b),且a+b=4.
如图,一次函数y=kx+3(k≠0)的图象经过点A(4,1),与x轴相交于点B,直线上有一点M(a,b),且a+b=4.