题目内容
如图，小俊在A处利用高为1.8米的测角仪AB测得楼EF顶部E的仰角为30°，然后前进12米到达C处，又测得楼顶E的仰角为60°，求楼EF的高度．（结果精确到0.1米）（参考数据：
=1.414，
=1.732）
【考点】解直角三角形的应用-仰角俯角问题．
【分析】设楼EF的高为x米，根据正切的概念用x表示出DG、BG，根据题意列出方程，解方程即可．
【解答】解：设楼EF的高为x米，则EG=EF﹣GF=（x﹣1.8）米，
由题意得：EF⊥AF，DC⊥AF，BA⊥AF，BD⊥EF，
在Rt△EGD中，DG=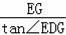
=
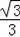
（x﹣1.8），
在Rt△EGB中，BG=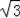
（x﹣1.8），
∴CA=DB=BG﹣DG=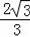
（x﹣1.8），
∵CA=12米，
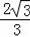
∴（x﹣1.8）=12，
解得：x=6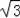
+1.8≈12.2，
答：楼EF的高度约为12.2米．
【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题，正确理解仰角和俯角的概念、熟记锐角三角函数的定义是解题的关键．
练习册系列答案
相关题目
+|1﹣4sin60°|+（2016π﹣
）0．
（x＞0）经过D点，交BC的延长线于E点，且OB•AC=160，有下列四个结论：
（x＞0）；②E点的坐标是（5，8）；③sin∠COA=
．其中正确的结论有（ ）
2011年北京春季房地产展示交易会期间，某公司对参加本次房交会的消费者的年收入和打算购买住房面积这两项内容进行了随机调查，共发放100份问卷，并全部收回．统计相关数据后，制成了如下的统计表和统计图：
消费者年收入统计表
| 年收入（万元） | 4.8 | 6 | 9 | 12 | 24 |
| 被调查的消费者数（人） | 10 | 50 | 30 | 9 | 1 |
请你根据以上信息，回答下列问题：
（1）补全统计表和统计图；
（2）打算购买住房面积小于100平方米的消费者人数占被调查人数的百分比为 ；
（3）求被调查的消费者平均每人年收入为多少万元？
，
B．
C．
