题目内容
2．
如图，AD，AE、CB均为⊙O的切线，D，E，F分别是切点，AD=8，则△ABC的周长为16．
分析 根据切线长定理得：EC=FC，BF=BD，AD=AE，再由△ABC的周长代入可求得结论．
解答 解：∵AD，AE、CB均为⊙O的切线，D，E，F分别是切点，
∴EC=FC，BF=BD，AD=AE，
∵△ABC的周长=AC+BC+AB=AC+CF+BF+AB，
∴△ABC的周长=AC+EC+BD+AB=AE+AD=2AD，
∵AD=8，
∴△ABC的周长为16．
点评 本题主要考查了切线长定理，熟练掌握从圆外一点引圆的两条切线，它们的切线长相等；此题运用线段间的等量代换将周长转化为一条线段长的2倍，得出结论．
练习册系列答案
相关题目
如图，在△ABC中，AB=AC，∠A=36°，线段AB的垂直平分线交AB于点D，交AC于点E，连结BE．求证：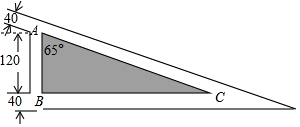
如图所示为某市生态绿化工程中的一幅大型绿化的平面图（单位：米）根据图示尺寸计算绿地（阴影部分-直角三角形）的面积（精确到0.1m）（参考数据sin65°=0.9063、cos65°=0.4226、tan65°=2.1445、cot65°=0.4663）
1．
某学生某月有零花钱a元，其支出情况如图所示，那么下列说法不正确的是（ ）
某学生某月有零花钱a元，其支出情况如图所示，那么下列说法不正确的是（ ）| A． | 捐赠款所对应的圆心角为240° | B． | 该学生捐赠款为0.6a元 | ||
| C． | 捐赠款是购书款的2倍 | D． | 其他消费占10% |
2．5的平方根是（ ）
| A． | $\sqrt{5}$ | B． | -$\sqrt{5}$ | C． | ±$\sqrt{5}$ | D． | 5 |