题目内容
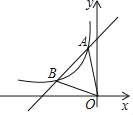
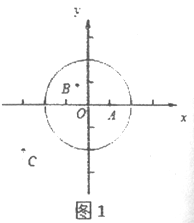
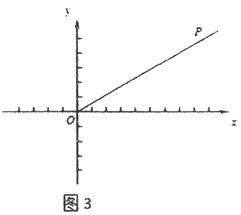
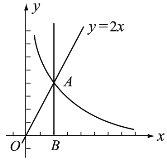
【题目】如图,点![]() 是直线
是直线![]() 与反比例函数
与反比例函数![]() (
(![]() 为常数)的图象的交点.过点
为常数)的图象的交点.过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,且
,且![]() .
.
(1)求点![]() 的坐标及
的坐标及![]() 的值;
的值;
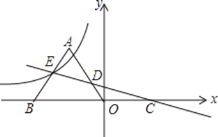
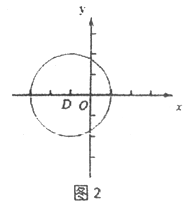
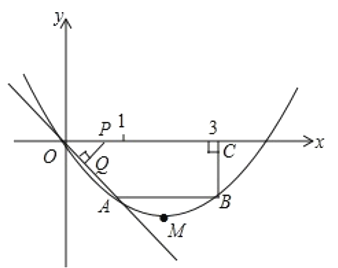
(2)已知点![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线,交直线
轴的直线,交直线![]() 于点
于点![]() ,交反比例函数
,交反比例函数![]() (
(![]() 为常数)的图象于点
为常数)的图象于点![]() ,交垂线
,交垂线![]() 于点
于点![]() .若
.若![]() ,结合函数的图象,直接写出
,结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)A(2,4);m=9;(2)6<x1+x2+x3≤7
【解析】
(1)由点A在正比例函数y=2x的图象上,可得点A的坐标为(2,4),再根据点A在反比例函数![]() 的图象上,即可得出m的值;
的图象上,即可得出m的值;
(2)依据x2<x3<x1,结合函数的图象,即可写出x1+x2+x3的取值范围.
解:(1)由题意得,可知点A的横坐标是2,
由点A在正比例函数y=2x的图象上,
∴点A的坐标为(2,4),
又∵点A在反比例函数![]() 的图象上,
的图象上,
∴4=![]() ,
,
即m=9;
(2)∵过点P(0,n)作平行于x轴的直线,交直线y=2x于点C(x1,y1),交反比例函数![]() (m为常数)的图象于点D(x2,y2),交垂线AB于点E(x3,y3),而x2<x3<x1,
(m为常数)的图象于点D(x2,y2),交垂线AB于点E(x3,y3),而x2<x3<x1,
∴4<n≤8,
∵当n=4时,x1+x2+x3=2+2+2=6;当n=8时,x1+x2+x3=4+1+2=7,
∴6<x1+x2+x3≤7.

练习册系列答案
相关题目
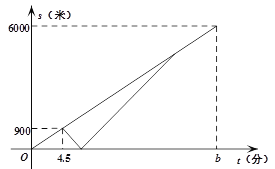
【题目】![]() ,
,![]() 两地相距
两地相距![]() ,甲、乙两人都由
,甲、乙两人都由![]() 地去
地去![]() 地,甲骑自行车,平均速度为
地,甲骑自行车,平均速度为![]() ;乙乘汽车,平均速度为
;乙乘汽车,平均速度为![]() ,且比甲晚
,且比甲晚![]() 出发.设甲的骑行时间为
出发.设甲的骑行时间为![]()
![]() .
.
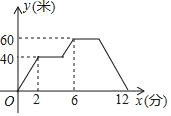
(1)根据题意,填写表格:
时间 与 | 0.5 | 1.8 | |
甲与 | 5 | 20 | |
乙与 | 0 | 12 |
(2)设甲,乙两人与![]() 地的距离为
地的距离为![]() 和
和![]() .写出
.写出![]() ,
,![]() 关于
关于![]() 的表达式;
的表达式;
(3)设甲,乙两人之间的距离为![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.