ћвƒњƒЏ»Ё
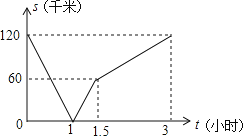
°Њћвƒњ°њ»зЌЉЉ„Ћщ Њ£ђ‘Џ∆љ√ж÷±љ«„ш±кѕµ÷–£ђ≈„ќпѕя![]() ”л
”л![]() ÷бљї”Џ
÷бљї”Џ![]() £ђ
£ђ![]() Ѕљµг£ђ”л
Ѕљµг£ђ”л![]() ÷бљї”Џµг
÷бљї”Џµг![]() £ђµг
£ђµг![]() ќ™Є√≈„ќпѕяµƒґ•µг£Ѓ
ќ™Є√≈„ќпѕяµƒґ•µг£Ѓ
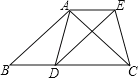
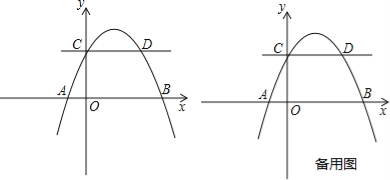
£®1£©»зЌЉЉ„£ђµг![]() ќ™≈„ќпѕя…ѕ
ќ™≈„ќпѕя…ѕ![]() £ђ
£ђ![]() ЅљµгЉдµƒ“їґѓµг£ђЅђљ”
ЅљµгЉдµƒ“їґѓµг£ђЅђљ”![]() £ђ
£ђ![]() £ђµ±
£ђµ±![]() √жїэ„оіу ±£ђ‘Џґ‘≥∆÷б…ѕ”–“їґѓµг
√жїэ„оіу ±£ђ‘Џґ‘≥∆÷б…ѕ”–“їґѓµг![]() £ђ»зЌЉ““Ћщ Њ£ђєэµг
£ђ»зЌЉ““Ћщ Њ£ђєэµг![]() „ч
„ч![]() ÷бљї
÷бљї![]() ÷б”Џµг
÷б”Џµг![]() £ђЅђљ”
£ђЅђљ”![]() £ђ
£ђ![]() £ђ«у
£ђ«у![]() µƒ„о–°÷µ£ђ≤Ґ«у≥ціЋ ±µг
µƒ„о–°÷µ£ђ≤Ґ«у≥ціЋ ±µг![]() µƒ„ш±к£ї
µƒ„ш±к£ї
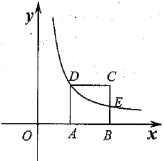
£®2£©»зЌЉ±ыЋщ Њ£ђљЂ![]() »∆„≈µг
»∆„≈µг![]() –э„™£ђµ√µљ
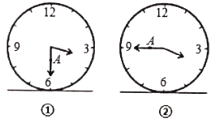
–э„™£ђµ√µљ![]() £ђ‘Џ–э„™єэ≥ћ÷–£ђ «Јсіж‘Џƒ≥Єц ±њћ є“‘µг
£ђ‘Џ–э„™єэ≥ћ÷–£ђ «Јсіж‘Џƒ≥Єц ±њћ є“‘µг![]() ќ™ґ•µгµƒ»эљ«–ќќ™“‘
ќ™ґ•µгµƒ»эљ«–ќќ™“‘![]() ќ™—ьµƒµ»—ь»эљ«–ќ£ђ»зєыіж‘Џ£ђ«л÷±љ”–і≥ціЋ ±µг
ќ™—ьµƒµ»—ь»эљ«–ќ£ђ»зєыіж‘Џ£ђ«л÷±љ”–і≥ціЋ ±µг![]() µƒ„ш±к£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£Ѓ
µƒ„ш±к£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£Ѓ
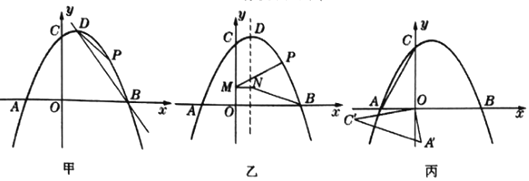
°Њір∞Є°њ£®1£©![]()
![]() £ї
£ї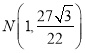 £ї£®2£©
£ї£®2£©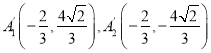 £ђ
£ђ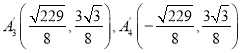 £Ѓ
£Ѓ
°Њљвќц°њ
£®1£©єэµг![]() „ч
„ч![]() ÷б”Џµг
÷б”Џµг![]() £ђљї
£ђљї![]() ”Џµг
”Џµг![]() £ђ”…
£ђ”…![]() √жїэ„оіу£ђµ√µљ
√жїэ„оіу£ђµ√µљ![]() „оіу£ђјы”√ґюіќЇѓ эµƒ–‘÷ µ√µљµг
„оіу£ђјы”√ґюіќЇѓ эµƒ–‘÷ µ√µљµг![]() µƒ„ш±к£ђљЂ
µƒ„ш±к£ђљЂ![]() ѕт„у∆љ“∆“їЄцµ•ќї£ђ єµг
ѕт„у∆љ“∆“їЄцµ•ќї£ђ єµг![]() ”Џµг
”Џµг![]() ÷ЎЇѕ£ђµг
÷ЎЇѕ£ђµг![]() ¬д‘Џ
¬д‘Џ![]() ÷б…ѕµƒµг
÷б…ѕµƒµг![]() і¶£ђµг
і¶£ђµг![]() єЎ”Џ
єЎ”Џ![]() ÷бґ‘≥∆µƒµгќ™
÷бґ‘≥∆µƒµгќ™![]() £ђіЋ ±
£ђіЋ ±![]() „о–°£ђ„о–°÷µќ™
„о–°£ђ„о–°÷µќ™![]() £ђі”ґшњ…µ√ір∞Є£ђ
£ђі”ґшњ…µ√ір∞Є£ђ
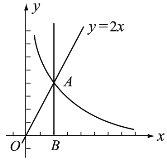
£®2£©–э„™єэ≥ћ÷–Ј÷Ѕљ÷÷«йњцћ÷¬џ£ђµ±![]() ±£ђ…и
±£ђ…и![]() £ђєэ
£ђєэ![]() „ч
„ч![]() ”Џ
”Џ![]() £ђєэ
£ђєэ![]() „ч
„ч![]() ”Џ
”Џ![]() јы”√ѕаЋ∆»эљ«–ќµƒ–‘÷ ±н Њ
јы”√ѕаЋ∆»эљ«–ќµƒ–‘÷ ±н Њ![]() µƒ„ш±к£ђјы”√єіє…ґ®јнљ®ЅҐЈљ≥ћ„й«уљвњ…µ√ір∞Є£ђµ±
µƒ„ш±к£ђјы”√єіє…ґ®јнљ®ЅҐЈљ≥ћ„й«уљвњ…µ√ір∞Є£ђµ±![]() Ќђјнњ…µ√ір∞Є£Ѓ
Ќђјнњ…µ√ір∞Є£Ѓ
љв£Ї£®1£©єэµг![]() „ч
„ч![]() ÷б”Џµг
÷б”Џµг![]() £ђљї
£ђљї![]() ”Џµг
”Џµг![]()
…и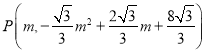 £ђ
£ђ
![]() £ђ
£ђ
![]() µ±
µ±![]()
![]()
Ѕо![]()
![]()
![]()
љвµ√£Ї![]()
![]()
…и![]() ќ™
ќ™![]()
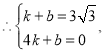
љвµ√£Ї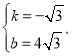
![]() ќ™
ќ™![]()
![]()
![]() £Ѓ
£Ѓ
![]()
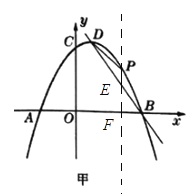
![]()
°аµ±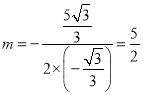 ±£ђ
±£ђ![]() „оіу£ђіЋ ±
„оіу£ђіЋ ±![]() µƒ√жїэ“≤„оіу£Ѓ
µƒ√жїэ“≤„оіу£Ѓ
іЋ ±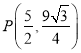
љЂ![]() ѕт„у∆љ“∆“їЄцµ•ќї£ђ єµг
ѕт„у∆љ“∆“їЄцµ•ќї£ђ єµг![]() ”Џµг
”Џµг![]() ÷ЎЇѕ£ђµг
÷ЎЇѕ£ђµг![]() ¬д‘Џ
¬д‘Џ![]() ÷б…ѕµƒµг
÷б…ѕµƒµг![]() і¶£ђ
і¶£ђ
µг![]() єЎ”Џ
єЎ”Џ![]() ÷бґ‘≥∆µƒµгќ™
÷бґ‘≥∆µƒµгќ™![]() £ђЅђљ”
£ђЅђљ”![]() љї
љї![]() ÷б”Џµг
÷б”Џµг![]() єэµг
єэµг![]() „ч
„ч![]() ÷б”Џµг
÷б”Џµг![]() £ђ
£ђ
іЋ ±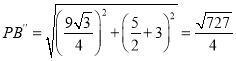
![]()
![]()
![]() £ђ
£ђ
![]()
![]() ќ™
ќ™![]() £ђ
£ђ
![]()
іЋ ±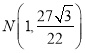
£®2£©”…ћв“в÷™£Ї![]()
![]()
µ±![]() ±£ђ
±£ђ
»зЌЉ£ђ…и![]() £ђєэ
£ђєэ![]() „ч
„ч![]() ”Џ
”Џ![]() £ђєэ
£ђєэ![]() „ч
„ч![]() ”Џ
”Џ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
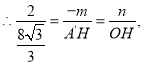
![]()
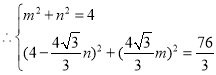
љвµ√£Ї
![]() їт
їт![]()
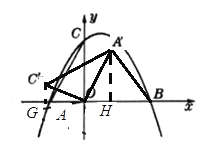
»зЌЉ£ђµ±![]()
Ќђјнњ…µ√£Ї
љвµ√£Ї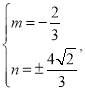
![]() їт
їт![]() £ђ
£ђ
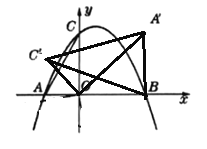
„џ…ѕ£Ї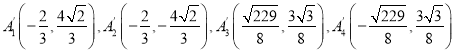

 ±Є’љ÷–њЉЇЃЉўѕµЅ–ір∞Є
±Є’љ÷–њЉЇЃЉўѕµЅ–ір∞Є