Question

【题目】，两地相距，甲、乙两人都由地去地，甲骑自行车，平均速度为；乙乘汽车，平均速度为，且比甲晚出发.设甲的骑行时间为．

（1）根据题意，填写表格：

时间 与地的距离（）	0.5	1.8
甲与地的距离	5		20
乙与地的距离	0	12

（2）设甲，乙两人与地的距离为和.写出，关于的表达式；

（3）设甲，乙两人之间的距离为，当时，求的取值范围.

Answer 1

【答案】（1）2，18，20；（2），；（3）或

【解析】

（1）根据“路程=速度×时间”公式以及题中所给时间和路程计算，可以得出表中数据；
（2）由（1）可得x=0．5时，，可求得；

因为前1.5个小时乙停留在原地没有出发，，当x=1.8时，，当x=2时，，即可求出

（3）甲，乙两人之间的距离为y实际上是y1，y2的差的绝对值．即可求得，当0x1.5时，由10x=12，得x=1．2，当1.5<x2时，由30x+60=12，得x=1.6，根据函数的增减性即可求得x的取值范围．

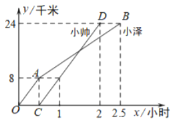
(Ⅰ)由题意知：甲、乙二人平均速度分别是平均速度为10km/h和40km/h，且比甲晚1.5h出发．

当时间x=1.8时，甲离开A的距离是10×1.8=18(km)
当甲离开A的距离20km时，甲的行驶时间是20÷10=2(时)
此时乙行驶的时间是21.5=0.5(时)，
所以乙离开A的距离是40×0.5=20(km)
故填写下表：

时间 与地的距离（）	0.5	1.8	2
甲与地的距离	5	18	20
乙与地的距离	0	12	20

(2)由（1）可得

当x=0.5时，

设y1=kx

∴5=0.5k

解得k=10

∴

∵前1．5个小时乙停留在原地没有出发

∴

当x=1.8时，，当x=2时，

设y2=mx+n

解得

∴

综上所述：

故答案为：，

(3)∵，

∴

当0x1.5时，由10x=12，得x=1.2

∵是增函数

∴若，则0x1.2

当1.5<x2时，由30x+60=12，得x=1.6

∵是减函数

∴若使，则1.6x2

综上所述：当时，求的取值范围为0x1.2或1.6x2

故答案为：0x1.2或1.6x2