题目内容
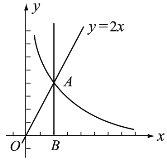
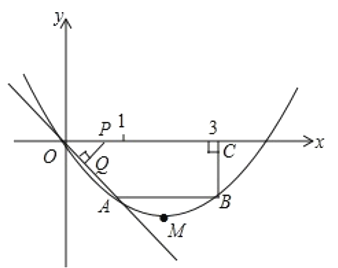
【题目】在四边形OABC中，AB∥OC，BC⊥x轴于C，A（1，-1），B（3，-1），动点P从O点出发，沿x轴正方向以3个单位/秒的速度运动．过P作PQ⊥OA于Q．设P点运动的时间为t秒（0 < t < 
），ΔOPQ与四边形OABC重叠的面积为S．
（1）求经过O、A、B三点的抛物线的解析式并确定顶点M的坐标；
（2）用含t的代数式表示P、Q两点的坐标；
（3）将ΔOPQ绕P点逆时针旋转90°，是否存在t，使得ΔOPQ的顶点O或Q落在抛物线上？若存在，直接写出t的值；若不存在，请说明理由；
（4）求S与t的函数解析式；
【答案】（1）
；顶点M的坐标为（2，
）；（2）P（3t，0），Q（
）；（3）存在，
或
；（4）
【解析】
（1）设抛物线的解析式为
，然后将点O、A、B的坐标代入即可求出结论；
（2）过点A作AH⊥x轴于H，过点Q作QN⊥x轴于N，证出△OAH为等腰直角三角形，∠AOH=45°，然后由题意易知OP=3t，△OPQ为等腰直角三角形，根据三线合一和直角三角形斜边上的中线等于斜边的一半即可求出结论；
（3）将△OPQ绕P点逆时针旋转90°，得到△O′PQ′，如下图所示，过点Q′作Q′K⊥x轴于K，根据题意即可求出O′的坐标，然后利用锐角三角函数即可求出Q′的坐标，然后根据O′在抛物线或Q′在抛物线分类讨论，代入解析式即可求出结论；
（4）根据t的取值分类讨论，分别画出对应的图形，根据三角形的面积、梯形的面积计算即可．
解：（1）设抛物线的解析式为
将点O、A、B的坐标代入，得
解得：
∴抛物线的解析式为
∵
∴顶点M的坐标为（2，）；
（2）过点A作AH⊥x轴于H，过点Q作QN⊥x轴于N
∵点A（1，-1）
∴AH=OH=1，
∴△OAH为等腰直角三角形，∠AOH=45°
∵动点P从O点出发，沿x轴正方向以3个单位/秒的速度运动，PQ⊥OA
∴OP=3t，△OPQ为等腰直角三角形
∴QN=ON=
OP=
∴点P的坐标为（3t，0），点Q的坐标为（，
）；
（3）将△OPQ绕P点逆时针旋转90°，得到△O′PQ′，如下图所示，过点Q′作Q′K⊥x轴于K
由题意可知：∠OPO′=∠QPQ′=90°，O′P=OP=3t，PQ′=PQ=OP·sin∠POQ=
∴∠Q′PK=180°－∠OPQ－∠QPQ′=45°，点O′的坐标为（3t，-3t）
∴PK=Q′K= PQ′·sin∠Q′PK=
∴OK=OP＋PK=
∴点Q′的坐标为（，）
当点O′在抛物线上时，则
解得：
（不符合题意，舍去）；
当点Q′在抛物线上时，则
解得：
（不符合题意，舍去）；
综上：当t=或时，△OPQ的顶点O或Q落在抛物线上
（4）由（3）知OP=3t，OQ=PQ=
根据勾股定理可得OA=
∴当点Q与点A重合时，
，解得：t=；
当点P与点C重合时3t=3，解得：t=1；
当0＜t≤时，如下图所示
S=OQ·PQ=××=
；
当＜t≤1时，如下图所示
∵AB∥OC
∴∠QAE=∠POQ=45°
易知EQ=AQ=OQ－OA=－
∴S=S△OPQ－S△AEQ
=OQ·PQ－AQ·EQ
=××－（－）（－）
=3t－1；
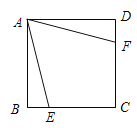
当1＜t＜
时，如下图所示，PQ分别与AB、BC交于点E、F
易知：OC=3，AB=3－1=2，BC=1，PC=3t－3，△PCF和△BEF为等腰直角三角形
∴CF=PC=3t－3，
∴BE=BF=BC－CF=4－3t
∴S=S梯形OABC－S△BEF
=BC（AB＋OC）－BE·BF
=×1×（2＋3）－（4－3t）（4－3t）
=
综上：
