题目内容
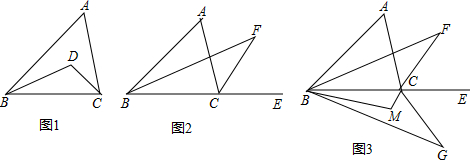
17.在△ABC中,已知∠A=α.(1)如图1,∠ABC、∠ACB的平分线相交于点D.
①当α=70°时,∠BDC度数=125度(直接写出结果);
②∠BDC的度数为90°+$\frac{1}{2}$α(用含α的代数式表示);
(2)如图2,若∠ABC的平分线与∠ACE角平分线交于点F,求∠BFC的度数(用含α的代数式表示).
(3)在(2)的条件下,将△FBC以直线BC为对称轴翻折得到△GBC,∠GBC的角平分线与∠GCB的角平分线交于点M(如图3),求∠BMC的度数(用含α的代数式表示).
分析 (1)①根据角平分线定义以及三角形内角和定理计算即可解决问题.
②根据角平分线定义以及三角形内角和定理计算即可解决问题.
(2)由∠BFC=∠FCE-∠FBC=$\frac{1}{2}(∠ACE-∠ABC)$由此即可解决问题.
(3)利用(2)的结论即可解决问题.
解答 解:(1)①125°;
②结论:${90°}+\frac{1}{2}α$,
理由:∵$∠DBC=\frac{1}{2}$∠ABC,∠DCB=$\frac{1}{2}$∠ACB,
∴∠BDC=180°-∠DBC-∠DCB=180°-$\frac{1}{2}$(∠ABC+∠ACB)=180°-$\frac{1}{2}$(180°-∠A)=90°+$\frac{1}{2}$∠A=90°+$\frac{1}{2}$α.
故答案分别为125°,90°+$\frac{1}{2}$α.
(2)∵BF和CF分别平分∠ABC和∠ACE
∴$∠FBC=\frac{1}{2}∠ABC$,$∠FCE=\frac{1}{2}∠ACE$,
∴∠BFC=∠FCE-∠FBC)=$\frac{1}{2}(∠ACE-∠ABC)$=$\frac{1}{2}∠A$
即$∠BFC=\frac{1}{2}α$.
(3)由轴对称性质知:$∠BGC=∠BFC=\frac{1}{2}α$,
由(1)②可得$∠BMC={90°}+\frac{1}{2}∠BGC$,
∴$∠BMC={90°}+\frac{1}{4}α$.
点评 本题考查三角形综合题、角平分线的性质、三角形内角和定理等知识,解题的关键是灵活运用三角形内角和定理解决问题,记住本题的两个基本结论,在以后学习中会有帮助的,属于中考常考题型.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
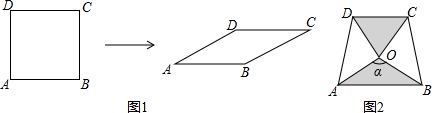
7.如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.
(1)请补全表:
(2)填空:
由(1)可以发现单位正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把单位菱形的面积S记为S(α).例如:当α=30°时,S=S(30°)=$\frac{1}{2}$;当α=135°时,S=S(135°)=$\frac{{\sqrt{2}}}{2}$.由上表可以得到S(60°)=S(120°);S(150°)=S(30°),…,由此可以归纳出S(180°-α)=(α°).
(3)两块相同的等腰直角三角板按图2的方式放置,AD=$\sqrt{2}$,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).

(1)请补全表:
| α | 30° | 45° | 60° | 90° | 120° | 135° | 150° |
| S | $\frac{1}{2}$ | 1 | $\frac{{\sqrt{2}}}{2}$ |
由(1)可以发现单位正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把单位菱形的面积S记为S(α).例如:当α=30°时,S=S(30°)=$\frac{1}{2}$;当α=135°时,S=S(135°)=$\frac{{\sqrt{2}}}{2}$.由上表可以得到S(60°)=S(120°);S(150°)=S(30°),…,由此可以归纳出S(180°-α)=(α°).
(3)两块相同的等腰直角三角板按图2的方式放置,AD=$\sqrt{2}$,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
 如图,三个正方形恰好围成一个直角三角形,它们的面积如图所示,则正方形A的面积为36.
如图,三个正方形恰好围成一个直角三角形,它们的面积如图所示,则正方形A的面积为36.