题目内容
1.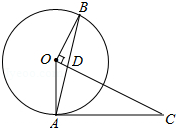 如图,△OAC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于B,垂足为O,连接AB交OC于点D,∠CAD=∠CDA.
如图,△OAC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于B,垂足为O,连接AB交OC于点D,∠CAD=∠CDA.(1)判断AC与⊙O的位置关系,并证明你的结论;
(2)若tan∠C=$\frac{3}{5}$,OD=1,求线段AC的长.
分析 (1)根据已知条件“∠CAD=∠CDA”、对顶角∠BDO=∠CDA可以推知∠BDO=∠CAD;然后根据等腰三角形OAB的两个底角相等、直角三角形的两个锐角互余的性质推知∠B+∠BDO=∠OAB+∠CAD=90°,即∠OAC=90°,可得AC是⊙O的切线;
(2)由tan∠C=$\frac{3}{5}$,可得$\frac{OA}{AC}$=$\frac{3}{5}$,则可设AC=5x,则AO=3x,由勾股定理,求得OC=$\sqrt{34}$x,继而可表示出AC=CD=5x,可得OC=5x+1,即可得方程$\sqrt{34}$x=5x+1,继而求得答案.
解答 (1)证明:∵∠CAD=∠CDA,∠BDO=∠CDA,
∴∠BDO=∠CAD,
又∵OA=OB,
∴∠B=∠OAB,
∵OB⊥OC,
∴∠B+∠BDO=∠OAB+∠CAD=90°,
即∠OAC=90°,
∴AC是⊙O的切线;
(2)解:在Rt△OAC中,∠OAC=90°,
∵tan∠C=$\frac{3}{5}$,
∴$\frac{OA}{AC}$=$\frac{3}{5}$,
∴设OA=3x,则AC=5x,
由勾股定理得:OC=$\sqrt{34}$x,
∵AC=CD,
∴AC=CD=5x,
∵OD=1,
∴OC=5x+1,
∴5x+1=$\sqrt{34}$x,
解得:x=$\frac{5+\sqrt{34}}{9}$,
∴AC=5x=$\frac{25+5\sqrt{34}}{9}$.
点评 此题考查了切线的性质与判定、勾股定理以及等腰三角形的性质.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
11.下列各图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.为体现党和政府对农民的关心,解决农民看病难的问题,某县于今年4月1日起开始全面实行新型农村合作医疗,对住院农民的医疗费实行分段报销制.下面是该县县级医疗机构住院病人累计分段报销表:
(1)农民刘老汉在4月份因病住院花去医疗费2200元,他可以报销多少元;
(2)如果住院花去医疗费10000元,他可以报销多少元?
(3)刘老汉在6月份因脑中风复发再次住院,这次报销医疗费4790.25元,刘老汉这次住院花去医疗费多少元?
| 医疗费 | 报销比例(%) |
| 500元以下(含500元) | 20% |
| 500元(不含)至2000元部分 | 30% |
| 2000元(不含)至5000元部分 | 35% |
| 5000元(不含)至10000元部分 | 40% |
| 10000元以上部分 | 45% |
(2)如果住院花去医疗费10000元,他可以报销多少元?
(3)刘老汉在6月份因脑中风复发再次住院,这次报销医疗费4790.25元,刘老汉这次住院花去医疗费多少元?
13.某同学利用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,列出的部分数据如下表:经检查,发现表格中恰好有一组数据计算错误,请你找出错误的那组数据是( )
| 序号 | ① | ② | ③ | ④ | ⑤ |
| x | 0 | 1 | 2 | 3 | 4 |
| y | 3 | 0 | -2 | 0 | 3 |
| A. | ① | B. | ② | C. | ③ | D. | ④ |
10. 如图,△OAD≌△OBC,∠O=50°,∠D=35°,则∠AEC等于( )
如图,△OAD≌△OBC,∠O=50°,∠D=35°,则∠AEC等于( )
 如图,△OAD≌△OBC,∠O=50°,∠D=35°,则∠AEC等于( )
如图,△OAD≌△OBC,∠O=50°,∠D=35°,则∠AEC等于( )| A. | 60° | B. | 50° | C. | 45° | D. | 30° |
11.一个扇形的圆心角为60°,它所对的弧长为2π,则这个扇形的半径为( )
| A. | 6 | B. | 2 | C. | 2$\sqrt{3}$ | D. | $\sqrt{6}$ |
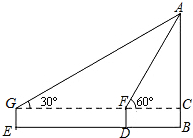 在学习解直角三角形的相关知识后,九年级1班的全体同学带着自制的测倾仪随老师来到了操场上,准备分组测量该校旗杆的高度,其中一个小组的同学在活动过程中获得了一些数据,并以此画出了如图所示的示意图,已知该组同学的测倾仪支杆长1m,第一次在D处测得旗杆顶端A的仰角为60°,第二次向后退12m到达E处,又测得旗杆顶端A的仰角为30°,求旗杆AB的高度.(结果保留根号)
在学习解直角三角形的相关知识后,九年级1班的全体同学带着自制的测倾仪随老师来到了操场上,准备分组测量该校旗杆的高度,其中一个小组的同学在活动过程中获得了一些数据,并以此画出了如图所示的示意图,已知该组同学的测倾仪支杆长1m,第一次在D处测得旗杆顶端A的仰角为60°,第二次向后退12m到达E处,又测得旗杆顶端A的仰角为30°,求旗杆AB的高度.(结果保留根号)