题目内容
10. 如图,△OAD≌△OBC,∠O=50°,∠D=35°,则∠AEC等于( )
如图,△OAD≌△OBC,∠O=50°,∠D=35°,则∠AEC等于( )| A. | 60° | B. | 50° | C. | 45° | D. | 30° |
分析 由三角形全等可知∠C=∠D=35°,在△OAD中,利用外角可求得∠EAC,在△AEC中利用三角形的内角和可求得∠AEC的度数.
解答 解:∵△OAD≌△OBC,
∴∠C=D=35°,
∴∠EAC=∠O+∠D=50°+35°=85°,
又∵∠AEC+∠EAC+∠C=180°,
∴∠AEC=180°-85°-35°=60°,
故选A.
点评 本题主要考查全等三角形的性质及外角的性质、三角形内角和定理,掌握全等三角形的对应角相等是解题的关键.

练习册系列答案
相关题目
18.计算$\frac{1}{a-1}-\frac{a}{a-1}$的结果是( )
| A. | -1 | B. | 1 | C. | $\frac{1+a}{a-1}$ | D. | 2 |
5.下列语句中,是命题的是( )
| A. | 两点确定一条直线吗? | B. | 在直线AB上取一点M | ||
| C. | 同一平面内,两条不相交的直线 | D. | 两个锐角的和大于直角 |
20.某时刻海上点P处有一客轮,测得灯塔A位于客轮P的北偏东30°方向,且相距20海里,客轮以60海里/小时的速度沿北偏西60°方向航行$\frac{2}{3}$小时到达B处,那么tan∠BAP=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
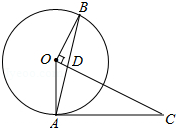 如图,△OAC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于B,垂足为O,连接AB交OC于点D,∠CAD=∠CDA.
如图,△OAC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于B,垂足为O,连接AB交OC于点D,∠CAD=∠CDA. 如图,△ABC中,∠ACB=80°,D为BC延长线上一点,且∠BAC=∠D,求∠BAD的度数.
如图,△ABC中,∠ACB=80°,D为BC延长线上一点,且∠BAC=∠D,求∠BAD的度数.