题目内容
2.若正整数n使得在计算n+1+n+2的过程中,各数位上均不产生进位现象,则称n为“本位数”.例如2和30是“本位数”,而5和91不是“本位数”.现从所有大于0且小于100的“本位数”中,随机抽取一个数,抽到偶数的概率为$\frac{9}{17}$.分析 先确定出所有大于0且小于100的“本位数”,再根据概率公式计算即可得解.
解答 解:所有大于0且小于100的“本位数”有:1、2、3、10、11、12、13、20、21、22、23、30、31、32,33、40、41、42、43,
共有17个,9个偶数,8个奇数,
所以,P(抽到偶数)=$\frac{9}{17}$,
故答案为:$\frac{9}{17}$.
点评 本题考查了概率公式,根据定义确定出所有的本位数是解题的关键,解题的易错点是忽略个位数上的进位.

练习册系列答案
相关题目
 如图所示,直线AD和BC被直线AB所截,∠1和∠2是同位角;∠4、∠FAC与∠2也是同位角.
如图所示,直线AD和BC被直线AB所截,∠1和∠2是同位角;∠4、∠FAC与∠2也是同位角.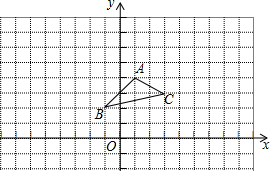 如图,在平面直角坐标系中,△ABC中的三个顶点坐标分别为A(1,4)、B(-1,2)、C(3,3).在x轴上方,请画出以原点O为位似中心,相似比为2:1.将△ABC放大后得到的△A1B1C1,并写出△A1B1C1各顶点的坐标.
如图,在平面直角坐标系中,△ABC中的三个顶点坐标分别为A(1,4)、B(-1,2)、C(3,3).在x轴上方,请画出以原点O为位似中心,相似比为2:1.将△ABC放大后得到的△A1B1C1,并写出△A1B1C1各顶点的坐标.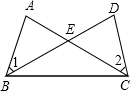 已知:如图,AB=DC,∠1=∠2.求证:∠EBC=∠ECB.
已知:如图,AB=DC,∠1=∠2.求证:∠EBC=∠ECB.