题目内容
11.已知:a=$\frac{1}{2+\sqrt{5}}$,b=$\frac{1}{2-\sqrt{5}}$,求2a2-5ab+2b2的值.分析 首先化简:a=$\frac{1}{2+\sqrt{5}}$=$\sqrt{5}$-2,b=$\frac{1}{2-\sqrt{5}}$=-2-$\sqrt{5}$,再进一步分解2a2-5ab+2b2=2(a-b)2-ab,代入求得答案即可.
解答 解:∵a=$\frac{1}{2+\sqrt{5}}$=$\sqrt{5}$-2,b=$\frac{1}{2-\sqrt{5}}$=-2-$\sqrt{5}$,
∴a-b=2$\sqrt{5}$,ab=-1,
∴2a2-5ab+2b2
=2(a-b)2-ab
=2×20+1
=41.
点评 此题考查二次根式的化简求值,此题注意借助因式分解的知识达到化简的目的.

练习册系列答案
相关题目
1.下列命题中真命题的个数是( )
①两个相似三角形的面积比等于相似比的平方;
②两个相似三角形对应高的比等于相似比;
③已知△ABC及位似中心O,能够作一个且只能作一个三角形,使位似比为0.5.
①两个相似三角形的面积比等于相似比的平方;
②两个相似三角形对应高的比等于相似比;
③已知△ABC及位似中心O,能够作一个且只能作一个三角形,使位似比为0.5.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
6.方程3x(x-1)=5(x-1)的根为( )
| A. | x=$\frac{5}{3}$ | B. | x=1 | C. | x1=1,x2=$\frac{5}{3}$ | D. | x1=1,x2=$\frac{3}{5}$ |
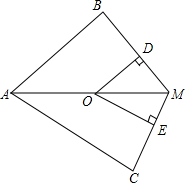 如图,已知AM平分∠BAC,点O是M上一点,OD⊥BM于点D,OE⊥CM于点E
如图,已知AM平分∠BAC,点O是M上一点,OD⊥BM于点D,OE⊥CM于点E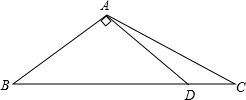 已知,如图△ABC中,AB=AC=10,BC=16,AD⊥AB于A,求CD的长.
已知,如图△ABC中,AB=AC=10,BC=16,AD⊥AB于A,求CD的长. 如图,△ABC≌△DBE,AB⊥BC,DE的延长线交AC于点F,那么DF⊥AC吗?说明理由.
如图,△ABC≌△DBE,AB⊥BC,DE的延长线交AC于点F,那么DF⊥AC吗?说明理由.