题目内容
4. 已知平行四边形ABCD,点E是BC边上的点,请回答下列问题:
已知平行四边形ABCD,点E是BC边上的点,请回答下列问题:(1)在图中求作$\overrightarrow{AD}$与$\overrightarrow{DC}$的和向量并填空:$\overrightarrow{AD}+\overrightarrow{DC}$=$\overrightarrow{AC}$;
(2)在图中求作$\overrightarrow{AD}$减$\overrightarrow{DC}$的差向量并填空:$\overrightarrow{AD}-\overrightarrow{DC}$=$\overrightarrow{BD}$;
(3)计算:$\overrightarrow{AB}+\overrightarrow{BE}+\overrightarrow{EA}$=$\overrightarrow{0}$.(作图不必写结论)
分析 (1)连接AC,根据向量的加减运算法则即可得出结论;
(2)连接BD,根据向量的加减运算法则即可得出结论;
(3)根据向量的加减运算法则即可得出结论.
解答 解:(1)连接AC,如图1所示.
$\overrightarrow{AD}$+$\overrightarrow{DC}$=$\overrightarrow{AC}$.
故答案为:$\overrightarrow{AC}$.
(2)连接BD,如图2所示.
∵$\overrightarrow{AD}$=$\overrightarrow{BC}$,-$\overrightarrow{DC}$=$\overrightarrow{CD}$,
∴$\overrightarrow{AD}$-$\overrightarrow{DC}$=$\overrightarrow{BC}$+$\overrightarrow{CD}$=$\overrightarrow{BD}$.
故答案为:$\overrightarrow{BD}$.
(3)∵$\overrightarrow{AB}$+$\overrightarrow{BE}$=$\overrightarrow{AE}$,$\overrightarrow{AE}$=-$\overrightarrow{EA}$,
∴$\overrightarrow{AB}$+$\overrightarrow{BE}$+$\overrightarrow{EA}$=$\overrightarrow{AE}$+$\overrightarrow{EA}$=$\overrightarrow{0}$.
故答案为:$\overrightarrow{0}$.
点评 本题考查了平面向量的加减运算以及平行四边形的性质,解题的关键是牢记平面向量的运算规则.本题属于基础题,难度不大,解决该题型题目时,在平行四边形中找出相等或相反的向量,再根据向量运算的规则进行运算是关键.

| A. | -3 | B. | 3 | C. | 0 | D. | $\sqrt{2}$ |
| A. | x=4 | B. | x=-4 | C. | x=8 | D. | x=-5 |
| A. | 110° | B. | 100° | C. | 80° | D. | 70° |




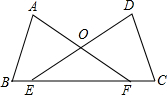 如图,点B、E、F、C在同一直线上,点A、D位于BC同侧,AB=DC,BE=CF,∠B=∠C.
如图,点B、E、F、C在同一直线上,点A、D位于BC同侧,AB=DC,BE=CF,∠B=∠C.