题目内容
如图,两个矩形如图(1)摆放,其中矩形ABCD的长a、宽b满足
+|b-
-1|=0,且另一矩形AEFG的宽AG和对角线FA长是方程x2-3x+2=0的两根
(1)分别求两个矩形的长、宽;
(2)求证△ABC∽△AGF;
(3)将图(1)中矩形AEFG绕A点逆时针旋转α角(0°<α<90°)得到图(2),连FC,M为FC中点,连EM、DM,问DM与EM有何数量关系?并证明你的结论.

a-3-
|
| 3 |
(1)分别求两个矩形的长、宽;
(2)求证△ABC∽△AGF;
(3)将图(1)中矩形AEFG绕A点逆时针旋转α角(0°<α<90°)得到图(2),连FC,M为FC中点,连EM、DM,问DM与EM有何数量关系?并证明你的结论.

考点:相似形综合题
专题:
分析:(1)根据非负数的性质可以得出
=0,|b-
-1|=0,就可以求出a、b的值,再通过解一元二次方程x2-3x+2=0求出其根就可以得出AG和对角线FA的值,由勾股定理就可以求出结论;
(2)由四边形AEFG和四边形ABCD是矩形可以得出∠G=∠B=90°,再由(1)的结论可以求出
=
,就可以求得△ABC∽△AGF;
(3)延长EM到N,使MN=ME,连接CN并延长交AB于H,连接DE、DN,根据条件可以得出△EFM≌△NCM,可以得出∠EFM=∠NCM,可以得出EF∥CN,运用条件可以证明△EAD∽△NCD,可以得出∠ADE=∠CDN,可以得出∠EDN=90°,根据直角三角形的性质就可以得出EM=DM.
a-3-
|
| 3 |
(2)由四边形AEFG和四边形ABCD是矩形可以得出∠G=∠B=90°,再由(1)的结论可以求出
| AB |
| AG |
| BC |
| GF |
(3)延长EM到N,使MN=ME,连接CN并延长交AB于H,连接DE、DN,根据条件可以得出△EFM≌△NCM,可以得出∠EFM=∠NCM,可以得出EF∥CN,运用条件可以证明△EAD∽△NCD,可以得出∠ADE=∠CDN,可以得出∠EDN=90°,根据直角三角形的性质就可以得出EM=DM.
解答:解:(1)∵
+|b-
-1|=0,
∴
=0,|b-
-1|=0,
∴a=3+
,b=
+1
∴BC=3+
,AB=
+1.
∵x2-3x+2=0的根为:
x1=1,x2=2,
∴AG=1,FA=2.
在Rt△AGF中,由勾股定理,得
FG=
.
∴矩形ABCD的长为3+
,宽为
+1,
矩形AEFG的长为
,宽为1;
(2)如图1,∵四边形AEFG和四边形ABCD是矩形,
∴∠G=∠B=∠ADC=90°,EF∥AG,DC∥AB.∠GAE=∠BAD=90°.
∵BC=3+
,AB=
+1.AG=1,GF=
,
∴
=
=
,
=
,
∴
=
,
∴△ABC∽△AGF;
(3)DM=EM.
理由:如图3,延长EM到N,使MN=ME,连接CN并延长交AB于H,连接DE、DN,
∵M为FC中点,
∴MF=MC.
∵在△EFM和△NCM中,
,
∴△EFM≌△NCM(SAS),
∴∠EFM=∠NCM,EF=CN=1
∴EF∥CH,
∴AG∥CH,
∴∠2=∠3.
∵.∠GAE+∠BAD+∠1+∠2=360°,
∴∠1+∠2=180°.
∵∠3+∠4=180°,
∴∠1=∠4.
∵DC∥AB,
∴∠4=∠DCH,
∴∠1=∠DCH.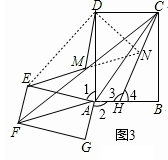
∵
=
=
,
=
=
,
∴
=
,
∴△EAD∽△NCD,
∴∠ADE=∠CDN.
∵∠ADN+∠CDN=∠ADC=90°,
∴∠ADN+∠ADE=90°,
即∠EDN=90°.
∵EM=NM,
∴DM=
EN,EM=
EN,
∴DM=EM.
a-3-
|
| 3 |
∴
a-3-
|
| 3 |
∴a=3+
| 3 |
| 3 |
∴BC=3+
| 3 |
| 3 |
∵x2-3x+2=0的根为:
x1=1,x2=2,
∴AG=1,FA=2.
在Rt△AGF中,由勾股定理,得
FG=
| 3 |
∴矩形ABCD的长为3+
| 3 |
| 3 |
矩形AEFG的长为
| 3 |
(2)如图1,∵四边形AEFG和四边形ABCD是矩形,
∴∠G=∠B=∠ADC=90°,EF∥AG,DC∥AB.∠GAE=∠BAD=90°.
∵BC=3+
| 3 |
| 3 |
| 3 |
∴
| GF |
| BC |
| ||
3+
|
| 1 | ||
|
| GA |
| AB |
| 1 | ||
|
∴
| GF |
| BC |
| GA |
| AB |
∴△ABC∽△AGF;
(3)DM=EM.
理由:如图3,延长EM到N,使MN=ME,连接CN并延长交AB于H,连接DE、DN,
∵M为FC中点,
∴MF=MC.
∵在△EFM和△NCM中,
|
∴△EFM≌△NCM(SAS),
∴∠EFM=∠NCM,EF=CN=1
∴EF∥CH,
∴AG∥CH,
∴∠2=∠3.
∵.∠GAE+∠BAD+∠1+∠2=360°,
∴∠1+∠2=180°.
∵∠3+∠4=180°,
∴∠1=∠4.
∵DC∥AB,
∴∠4=∠DCH,
∴∠1=∠DCH.

∵
| EA |
| CN |
| ||
| 1 |
| 3 |
| DA |
| CD |
3+
| ||
|
| 3 |
∴
| EA |
| CN |
| DA |
| CD |
∴△EAD∽△NCD,
∴∠ADE=∠CDN.
∵∠ADN+∠CDN=∠ADC=90°,
∴∠ADN+∠ADE=90°,
即∠EDN=90°.
∵EM=NM,
∴DM=
| 1 |
| 2 |
| 1 |
| 2 |
∴DM=EM.
点评:本题是一道相似形的综合试题,考查了非负数的性质的运用,一元二次方程的解法及运用,勾股定理的运用,相似三角形的判定及性质的运用,直角三角形的性质的运用,全等三角形的判定及性质的运用,解答时根据条件证明三角形全等和三角形相似是解答本题的关键.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,AB=d,过A作⊙O的切线并在其上取一点C,使AC=AB,连接OC交⊙O于点D,BD的延长线交AC于E.
如图,AB是⊙O的直径,AB=d,过A作⊙O的切线并在其上取一点C,使AC=AB,连接OC交⊙O于点D,BD的延长线交AC于E. 如图,在平面直角坐标系中,点A,C分别在x轴,y轴上,四边形ABCO为矩形,AB=4,BC=3,点D与点A关于y轴对称,点E,F分别是线段AD,AC上的动点(点E不与点A,D重合),且∠CEF=∠ACB.
如图,在平面直角坐标系中,点A,C分别在x轴,y轴上,四边形ABCO为矩形,AB=4,BC=3,点D与点A关于y轴对称,点E,F分别是线段AD,AC上的动点(点E不与点A,D重合),且∠CEF=∠ACB.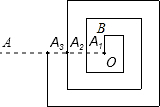 如图是一个回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A1、A2、A3…若从O到点A1的回形线为第一圈(长为7),从点A1到A2为第二圈,…以此类推,则第10圈的线长为( )
如图是一个回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A1、A2、A3…若从O到点A1的回形线为第一圈(长为7),从点A1到A2为第二圈,…以此类推,则第10圈的线长为( ) 已知如图,点P是反比例函数上的任意一点,过点P作x轴的垂线,垂足为A,连接OP.若△PAO的面积是3,那么该反比例函数在第二象限的表达式为
已知如图,点P是反比例函数上的任意一点,过点P作x轴的垂线,垂足为A,连接OP.若△PAO的面积是3,那么该反比例函数在第二象限的表达式为