题目内容
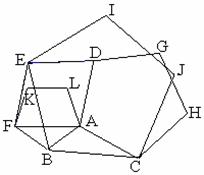
在△ABC中,AB=AC=5,BC=6,以AC为一边作正方形ACDE,过点D作DF⊥BC交直线BC于点F,连接AF,请你画出图形,直接写出AF的长,并画出体现解法的辅助线.
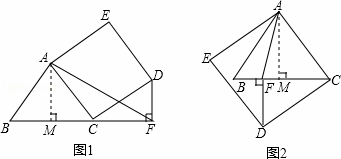
解:如图1所示:
∵AB=AC=5,BC=6,
∴AM=4,
∵∠ACM+∠DCF=90°,∠MAC+∠ACM=90°,
∴∠CAM=∠DCF,
在△AMC和△CFD中
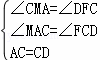 ,
,
∴△AMC≌△CFD(AAS),
∴AM=CF=4,
故AF=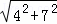 =
=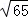 ,
,
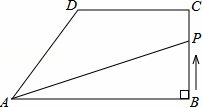
如图2所示:
∵AB=AC=5,BC=6,
∴AM=4,MC=3,
∵∠ACM+∠DCF=90°,∠MAC+∠ACM=90°,
∴∠CAM=∠DCF,
在△AMC和△CFD中
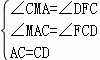 ,
,
∴△AMC≌△CFD(AAS),
∴AM=FC=4,
∴FM=FC﹣MC=1,
故AF=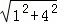 =
=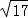 .
.
注:每图1分(图1中没有辅助线、没有直角符号均不给分;图2中没有辅助线、没有直角符号、点B在正方形外均不给分).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
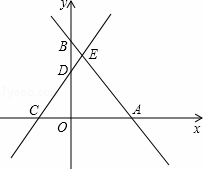
若将抛物线y=x2向右平移2个单位,再向上平移3个单位,则所得抛物线的表达式为( )
|
| A. | y=(x+2)2+3 | B. | y=(x﹣2)2+3 | C. | y=(x+2)2﹣3 | D. | y=(x﹣2)2﹣3 |