题目内容
如图,以△ABC的各边为边,在BC的同侧分别作三个正五边形.它们分别是正五边形ABFKL、BCJIE、ACHGD,试探究:
(1)四边形ADEF是什么四边形?
(2)当△ABC满足什么条件时,四边形ADEF是正方形?
(不需证明)
(3)四边形ADEF一定存在吗?为什么?
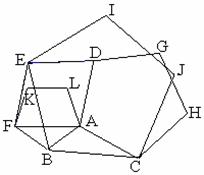
(1)∵正五边形ABFKL、BCJIE, ∴BF=BA,BE=BC----------1分
又∵∠3=108°-∠2=∠1-------------1分; ∴△FBE≌△ABC∴EF=AC,∠4=∠5
∵正五边形ACHGD,∴AC=DA, ∴EF=DA--------------------1分;
又∵∠FAD=360°-∠BAF-∠4-∠CAD=360°-36°-108°-∠4=216°-∠4;
∠EFA=∠5-∠AFB=∠5-36°;
∴∠FAD+∠EFA=216°-∠4+∠5-36°=180°,
∴EF∥DA,∴四边形ADEF是平行四边形;-----------------3分
(2)当∠BAC=126°,且AB=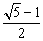 AC(或AC=2cos36°)时,四边形ADEF是正方形;-------(两个条件各2分,共4分)
AC(或AC=2cos36°)时,四边形ADEF是正方形;-------(两个条件各2分,共4分)
(3)当∠BAC=36°时,点D、A、F在同一直线上,以A,D,E,F为顶点的四边形不存在(2分)

练习册系列答案
相关题目
用4个完全相同的小正方体组成如图所示的立方体图形,它的俯视图是( )

|
| A. |
| B. |
| C. |
| D. |
|




 ,∠B=30º, AD平分∠
,∠B=30º, AD平分∠ ,CD=2 cm,则BD的长是_______
,CD=2 cm,则BD的长是_______ 
 ,其中
,其中 60°
60°

 30°,请你取一个合适的数作为
30°,请你取一个合适的数作为




 的解集在数轴上表示正确的是 ( )
的解集在数轴上表示正确的是 ( ) 